พื้นฐานทางกายภาพของมอเตอร์ไฟฟ้า

1. หลักการทางกายภาพของการทำงานของมอเตอร์ไฟฟ้า

1.1 ระบบสมการของแมกซ์เวลล์

มอเตอร์ไฟฟ้าเป็นทรานสดิวเซอร์ที่แปลงพลังงานแม่เหล็กไฟฟ้าและพลังงานกลอย่างต่อเนื่อง

เมื่อป้อนพลังงานไฟฟ้า มอเตอร์ไฟฟ้าสามารถส่งแรงบิดและพลังงานกลออกมาอย่างต่อเนื่อง

เช่น มอเตอร์ไฟฟ้า ในทางกลับกัน หากแรงภายนอกผลักเพลาของมอเตอร์ไฟฟ้าอย่างต่อเนื่องและป้อนพลังงานกลเข้าไป มอเตอร์ไฟฟ้าสามารถส่งแรงดันและพลังงานไฟฟ้าออกจากปลายสายได้อย่างต่อเนื่องในลักษณะย้อนกลับ นั่นคือ เครื่องกำเนิดไฟฟ้า

ในอดีต หม้อแปลงไฟฟ้าสถิตยังถูกนับเป็นมอเตอร์ไฟฟ้าด้วย แต่ค่อยๆ พัฒนาเพื่ออ้างถึงมอเตอร์ไฟฟ้าและเครื่องกำเนิดไฟฟ้าเท่านั้น

ข้อดีอย่างหนึ่งของมอเตอร์ไฟฟ้าคือการสูญเสียค่อนข้างน้อย จึงมีประสิทธิภาพสูง

มอเตอร์ไฟฟ้าขนาดใหญ่สามารถบรรลุประสิทธิภาพได้สูงถึง 99%

เมื่อพูดถึงระบบแม่เหล็กไฟฟ้า ระบบสมการของแมกซ์เวลล์คงหนีไม่พ้น

ในโลกมหภาคและแม้ในโลกจุลภาค

ระบบสมการของแมกซ์เวลล์สามารถอธิบายคุณสมบัติของระบบได้อย่างมีประสิทธิภาพมาก

ระบบสมการของแมกซ์เวลล์สรุปได้จากการศึกษาปรากฏการณ์แม่เหล็กไฟฟ้าก่อนหน้านี้

มีสมการพื้นฐานสี่สมการทั้งในรูปดิฟเฟอเรนเชียลและอินทิกรัล

ทีนี้ลองตรวจสอบระบบสมการของแมกซ์เวลล์ในรูปแบบอินทิกรัลกัน

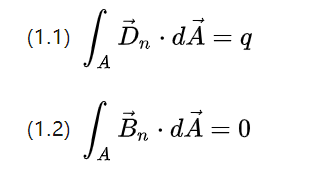
สมการสองสมการด้านบนอธิบายฟลักซ์ของความหนาแน่นของสนาม ตามลำดับ รวมของภาพการเปลี่ยนแปลงศักย์ไหลออก และภาพการเหนี่ยวนำสนามแม่เหล็กหมุนทั้งหมดในพื้นที่ปิด

ตามความรู้ที่เรียนในโรงเรียนมัธยม สนามไฟฟ้าสามารถสร้างขึ้นโดยการกระตุ้นจุดประจุ สนามแม่เหล็กไม่สามารถถูกกระตุ้นโดยโมโนโพลแม่เหล็ก แต่เพื่อขยายเส้นทางปิด ดังนั้นสนามไฟฟ้าจึงทำงานอยู่ สนามแม่เหล็กคือ เฉยเมย

ดังนั้นฟลักซ์การเลื่อนที่อาจเกิดขึ้นทั้งหมดคือประจุทั้งหมด q และฟลักซ์แม่เหล็กทั้งหมดคือ 0

สมการสองสมการข้างต้นอธิบายปริมาณการหมุนของความเข้มของสนาม ปริพันธ์ของความเข้มของสนามไฟฟ้าทั้งหมด และความเข้มของสนามแม่เหล็กทั้งหมด

สอดคล้องกับอัตราการเปลี่ยนแปลงของฟลักซ์แม่เหล็กและอัตราการเปลี่ยนแปลงของการเปลี่ยนแปลงที่อาจเกิดขึ้น (ความเข้มของกระแส) ตามลำดับ สำหรับหนึ่งรอบตามเส้นทางของเส้นโค้งบนเส้นโค้งพื้นที่ปิด

สูตรเกาส์และสโตกส์ยังช่วยให้สามารถเขียนสมการทั้งสี่ข้างต้นใหม่ในรูปแบบดิฟเฟอเรนเชียลได้ดังนี้

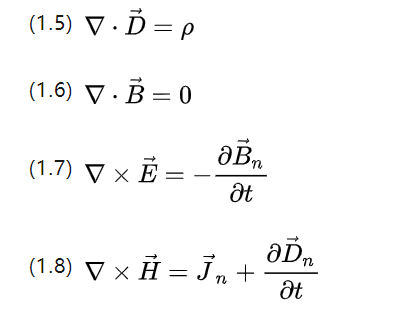
▽ สำหรับตัวดำเนินการ Nabla โดยใช้เวกเตอร์ดอทโปรดักต์เพื่อคำนวณสแกตเตอร์และผลคูณทางแยกเพื่อคำนวณสปิน P สำหรับความหนาแน่นของประจุไฟฟ้า และ Jn สำหรับความหนาแน่นกระแส

สมการข้างต้นสามารถอธิบายพฤติกรรมแม่เหล็กไฟฟ้าทั้งหมดที่เกิดขึ้นในระบบมอเตอร์เหนี่ยวนำไฟฟ้ากระแสสลับโดยทั่วไป

1.2 โพลาไรเซชันของวัสดุและการทำให้เป็นแม่เหล็กสำหรับพลังงานไฟฟ้า

ในสนามแม่เหล็กหมุนด้วยไฟฟ้าที่ใช้ โมเลกุลของวัสดุจะเปลี่ยนทิศทางเนื่องจากขั้วได้รับผลกระทบจากความแรงของสนาม

โดเมนทางไฟฟ้าที่เกิดจากกลุ่มโมเลกุลดั้งเดิมที่มีขนาดต่างๆ ไม่เท่ากันจะถูกโพลาไรซ์เนื่องจากสนามแม่เหล็กที่ใช้ และทิศทางการกระจายประจุจะบรรจบกัน

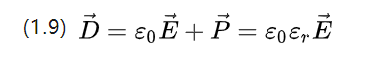
E0=8.854187817*10-12F/m คือค่าความอนุญาตของสุญญากาศ ซึ่งเป็นค่าคงที่ไดอิเล็กตริกของสุญญากาศด้วย และ P คือค่าคงที่ไดอิเล็กตริกสัมพัทธ์ ซึ่งกำหนดโดยคุณสมบัติของวัสดุเอง

(1.9) อธิบายถึงความหนาแน่นของการเลื่อนศักย์ของสนามไฟฟ้าที่ใช้และภาพความเข้มของโพลาไรเซชันที่สอดคล้องกัน

ในสนามแม่เหล็กที่ใช้ โดเมนแม่เหล็กที่สอดคล้องกันและความแรงของแม่เหล็กสามารถรับได้ในลักษณะเดียวกัน

ซึ่งแตกต่างจากสนามไฟฟ้า ความเข้มของโพลาไรซ์แม่เหล็ก M ถูกนำมาใช้ ซึ่งอธิบายถึงความแตกต่างระหว่างความแรงของการเหนี่ยวนำแม่เหล็กของวัสดุกับสภาพแวดล้อมของสุญญากาศ

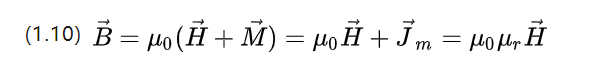
U0=4π*10-7 N.A-2 คือความสามารถในการซึมผ่านของสุญญากาศ และ Ur คือความสามารถในการซึมผ่านสัมพัทธ์ ซึ่งอธิบายถึงความสามารถของวัสดุในการยอมให้สนามแม่เหล็กผ่านได้

ถ้าคุณ<=1 เป็นสารต้านแม่เหล็ก วัสดุป้องกันการผ่านของสนามแม่เหล็ก หากภาพเป็นพาราแมกเนติก วัสดุนั้นจะเป็นไปตามเส้นทางผ่านของสนามแม่เหล็ก

ถ้าคุณ>=1o 5 เป็นเฟอร์โรแมกเนติก วัสดุเช่น เฟอร์โร-โคบอลต์ นิเกิล จะเพิ่มสนามแม่เหล็กหลังจากการทำให้เป็นแม่เหล็ก จากนั้นจึงรักษาความแรงของสนามแม่เหล็กไว้หลังจากเอาสนามแม่เหล็กออกแล้ว ซึ่งเรียกว่าแม่เหล็กที่เหลืออยู่

ในกระบวนการของการทำงานของมอเตอร์จะมีการดึงดูดและล้างอำนาจแม่เหล็กอย่างต่อเนื่อง ดังนั้นควรให้ความสนใจกับการตรวจสอบเส้นฮิสเทรีซิสของวัสดุต่างๆ

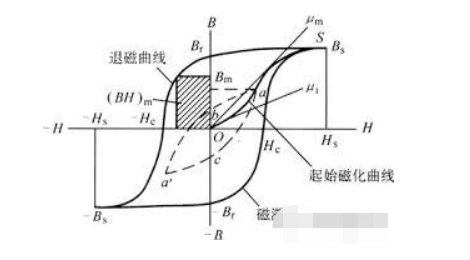
เส้นฮิสเทรีซิสอธิบายถึงการเหนี่ยวนำแม่เหล็กที่เพิ่มขึ้นของวัสดุแม่เหล็กเมื่อความแรงของสนามเพิ่มขึ้นภายใต้การกระทำของสนามแม่เหล็กที่ใช้ความแรง H

การเหนี่ยวนำแม่เหล็กนี้ไม่เป็นไปตามความแรงของสนามหลังจากถึงจุดอิ่มตัวของสนามแม่เหล็ก

หลังจากถึงจุดอิ่มตัวของสนามแม่เหล็กแล้ว เป็นเรื่องยากที่จะติดตามความแรงของสนามแม่เหล็กที่เพิ่มขึ้น เมื่อความแรงของสนามแม่เหล็กภายนอกค่อยๆ ลดลงจนเป็นศูนย์ จะเห็นได้ว่าเส้นโค้งการล้างอำนาจแม่เหล็กยังคงรักษาสภาพแม่เหล็กที่เหลืออยู่ B เมื่อผ่านจุดศูนย์

การดึงดูดแม่เหล็กที่เหลืออยู่นี้แสดงหลักการทั่วไปของการผลิตแม่เหล็กถาวร นั่นคือ การดึงดูดแม่เหล็กแบบกำหนดทิศทางตามด้วยการล้างอำนาจแม่เหล็กอย่างค่อยเป็นค่อยไป เมื่อใช้สนามแม่เหล็กผกผัน ความแรงของการเหนี่ยวนำแม่เหล็กจะเป็นศูนย์หรือเพิ่มขึ้นในทิศทางตรงกันข้าม และส่วนเกินนี้เรียกว่า coercivity H

1.3 แรงแม่เหล็กไฟฟ้าและพลังงานกล

คุณค่าสูงสุดของมอเตอร์คือการตระหนักถึงการแปลงพลังงานไฟฟ้าเป็นพลังงานกล เพื่อทำงานภายนอกและดำเนินการเคลื่อนไหวตามเป้าหมาย

การเคลื่อนที่ของอนุภาคที่มีประจุในสนามแม่เหล็กขึ้นอยู่กับแรงลอเรนซ์ที่ตั้งฉากกับทิศทางการเคลื่อนที่ ซึ่งการแสดงออกทางมหภาคคือแรงแอมแปร์ Hm = Il * B ซึ่งสามารถตัดสินได้โดยใช้กฎมือซ้ายเพื่อกำหนด ทิศทาง,

I คือความยาวที่มีประสิทธิภาพของตัวนำในสนามแม่เหล็กในทิศทางของกระแส

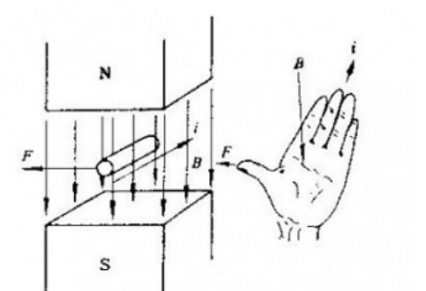
นอกจากนี้ยังมีแรงสนามไฟฟ้าที่สอดคล้องกันในสนามไฟฟ้าสถิต Fe=qE .

และทั้งสนามแม่เหล็กและสนามไฟฟ้าต่างก็เป็นสนามในตัวเอง และแรงที่กระทำต่อประจุหรือองค์ประกอบกระแสในพวกมันนั้นขึ้นอยู่กับปริมาตรและความหนาแน่นของสนาม ดังนั้น สามารถตรวจสอบแรงสนามที่สอดคล้องกันในรูปของสนามได้

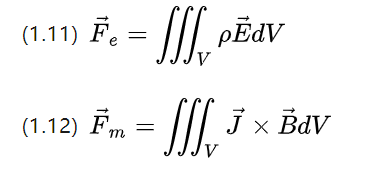
สมการทั้งสองข้างต้นยังคงรักษาความสมมาตร ความหนาแน่นของประจุ P ในปริมาตรหนึ่งเนื่องจากความแรงของสนามไฟฟ้าทำให้ความหนาแน่นของแรงไฟฟ้า fe = pE

ความหนาแน่นกระแส J ในปริมาตรหนึ่งเนื่องจากความแรงของสนามแม่เหล็กทำให้เกิดความหนาแน่นของแรงแม่เหล็ก Fm = J * B (ต้องใช้สมการข้างต้น (1.12) ในกรณีของวัสดุไอโซทรอปิกและกระแสคงที่)

การแสดงออกนี้เป็นแรงบันดาลใจให้เราตรวจสอบพลังงานและความหนาแน่นของพลังงานของสนามแม่เหล็กไฟฟ้าโดยตรง

ด้วยวิธีนี้ พลังงานศักย์แม่เหล็กไฟฟ้า ณ จุดหนึ่งสามารถหาได้โดยการหาเกรเดียนต์เพื่อให้ได้ความหนาแน่นของแรงแม่เหล็กไฟฟ้าที่สอดคล้องกัน และด้วยเหตุนี้จึงหาแรงแม่เหล็กไฟฟ้าทั้งหมดบนวัตถุที่กำลังตรวจสอบ

1.4 แบบคอยล์

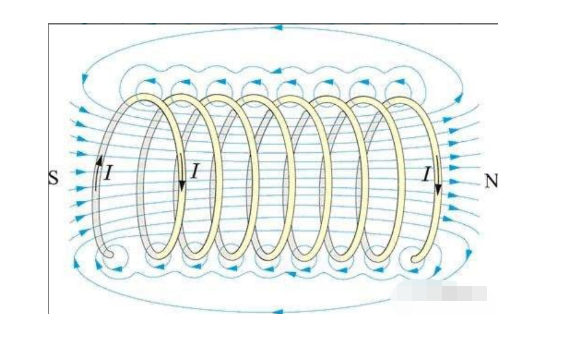
ขดลวดเป็นองค์ประกอบพื้นฐานที่สร้างแบบจำลองของมอเตอร์เหนี่ยวนำ เชื่อมโยงแบบจำลองวงจรของมอเตอร์กระแสสลับกับแบบจำลองทางกายภาพของวัตถุ

ส่วนที่เป็นเส้นตรงของตัวนำที่มีพลังงานจะสร้างสนามแม่เหล็กแบบวงแหวนรอบๆ (ตามสมการ 1.4)

เมื่อตัวนำถูกปิดที่จุดเริ่มต้นและจุดสิ้นสุด สนาม Toroidal จะสร้างเส้นแรงแม่เหล็กที่ศูนย์กลางของวงแหวนตัวนำที่ผ่านในแนวตั้งผ่านวงแหวนตัวนำ เช่น โซลินอยด์

พิจารณาเฉพาะกระแสบนตัวนำที่มีพลังงาน (1.4) ลดความซับซ้อนเป็น:

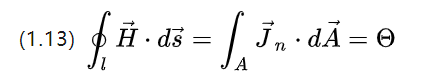
แรงแม่เหล็ก (magnetische Durchfluchtung) ซึ่งเป็นที่มาของความแรงของสนามกระตุ้น โดยพื้นฐานแล้วคือความแรงของกระแสทั้งหมดที่ไหลผ่านส่วนของตัวนำแบบปิดใน [A]

เนื่องจากในทางปฏิบัติลวดที่มีพลังงานจะพันเป็นขดลวด กระแสของลวดจึงแยกจากกัน และ (1.13) จึงเขียนใหม่เป็น

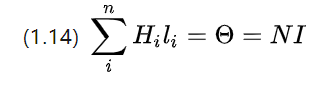
N คือจำนวนขดลวดทั้งหมดในขดลวด นั่นคือจำนวนรอบ

จะเห็นได้ว่าหากจำนวนรอบสูงขึ้น กระแสรวมจะสูงขึ้น ศักย์แม่เหล็กก็จะสูงขึ้น และสนามแม่เหล็กก็จะยิ่งแรงขึ้นเท่านั้น

ขดลวดแบบหมุนรอบเดียวในสนามแม่เหล็กที่แปรผันตามเวลาจะเหนี่ยวนำให้เกิดแรงดันไฟฟ้าที่ปลายทั้งสองของเส้นลวด ซึ่งเป็นปรากฏการณ์ที่อธิบายโดย (1.3)

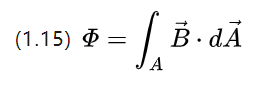
เป็นที่เข้าใจได้ว่าการเหนี่ยวนำแม่เหล็กสามารถตีความได้ว่าเป็นความหนาแน่นฟลักซ์แม่เหล็กซึ่งสามารถรับได้โดยการแทนที่ (1.3)

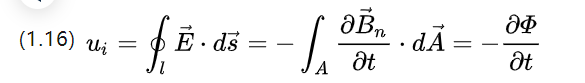
Ui คือศักย์ไฟฟ้าเหนี่ยวนำ พิจารณาการเปลี่ยนแปลงของฟลักซ์ได้ 2 รูปแบบ รูปแบบหนึ่งคือเปลี่ยนบริเวณขดลวดแต่เปลี่ยนความหนาแน่นของฟลักซ์ ดังนี้

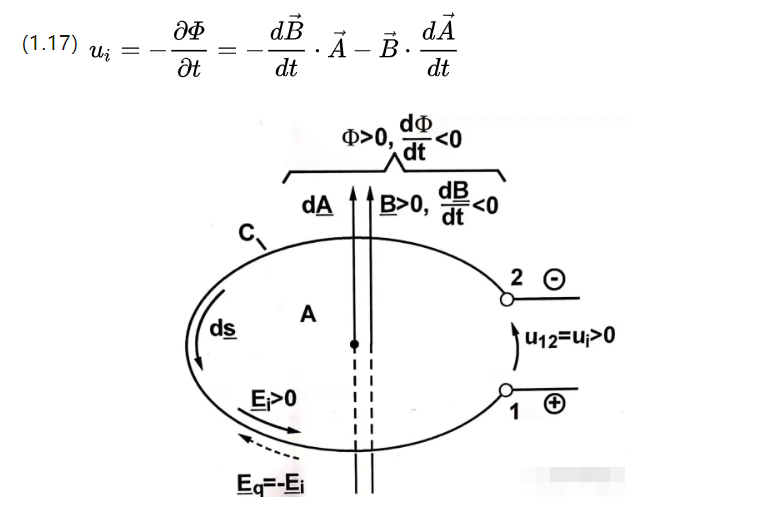
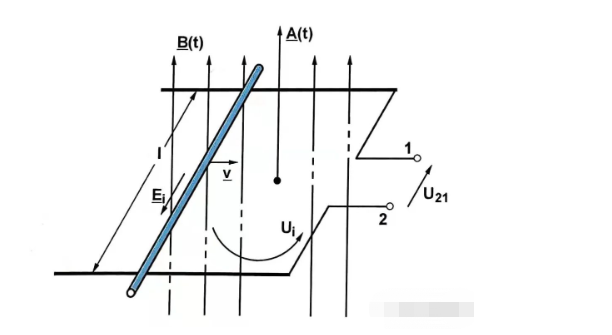
ส่วนแรกคือศักยภาพการเหนี่ยวนำที่เปลี่ยนรูปแบบอย่างเป็นทางการ และส่วนหลังคือศักยภาพการเหนี่ยวนำที่แปรเปลี่ยนโดยการแปล

แบบแรกมีความหนาแน่นของฟลักซ์แม่เหล็กที่แปรผันตามเวลา ในขณะที่แบบหลังมีพื้นที่คอยล์ที่มีประสิทธิภาพแปรผันตามเวลา

หลักการอุปนัยนี้ถูกกล่าวถึงในฟิสิกส์ระดับมัธยมปลายและเป็นที่รู้จักกันว่าทฤษฎีบทฟลุต

เมื่อขดลวดมีหลายรอบ ฟลักซ์ที่มีประสิทธิผลทั้งหมดจะเป็นจำนวนเต็มทวีคูณของการหมุนของขดลวดที่ขยาย ดังนั้น จึงแนะนำแนวคิดของโซ่แม่เหล็ก

โซ่ถูกกำหนดไว้ในรูปด้านล่าง

โปรดทราบว่าสายโซ่แม่เหล็กเป็นปริมาณสเกลาร์ เช่นเดียวกับฟลักซ์แม่เหล็ก เนื่องจากการเปลี่ยนแปลงของกระแสสามารถทำให้เกิดการเปลี่ยนแปลงของฟลักซ์ได้ แนวโน้มที่จะขัดขวางการเปลี่ยนแปลงของฟลักซ์ ซึ่งสามารถกำหนดเป็น:

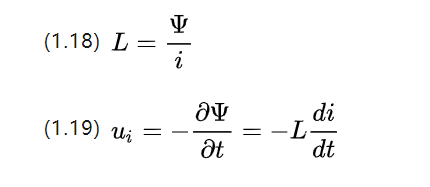
i คือความเข้มกระแสที่แตกต่างกัน L คือค่าสัมประสิทธิ์การเหนี่ยวนำตัวเองใน Henry [H] และขนาดของมันสัมพันธ์กับรูปร่างปริมาตรของขดลวด จำนวนรอบ และการซึมผ่านของแม่เหล็ก

คอยล์ในมอเตอร์เหนี่ยวนำถูกผลิตขึ้นเพื่อให้มีวัสดุแม่เหล็กไฟฟ้าอยู่ตรงกลางของขดลวด เช่น แกนเหล็ก เพื่อเพิ่มการซึมผ่านของแม่เหล็ก เพื่อให้ขดลวดพันบนแกนเหล็ก จึงมีชื่อว่า ขดลวด

สำหรับส่วนของวัสดุที่เป็นเนื้อเดียวกันเชิงเส้น ค่าสัมประสิทธิ์การเหนี่ยวนำตัวเองสามารถประมาณได้ด้วยสมการต่อไปนี้

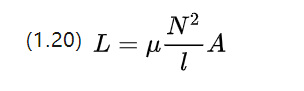
ตัวเหนี่ยวนำตัวเองเป็นขดลวดของการเปลี่ยนแปลงในปัจจุบันของตัวเองเพื่อเหนี่ยวนำปรากฏการณ์ของแรงดันปราบปราม แนวโน้มที่จะขัดขวางการเปลี่ยนแปลงในปัจจุบันเกี่ยวกับมอเตอร์ไฟฟ้ากระแสตรง..

เมื่อสองขดลวดอยู่ใกล้กัน นอกเหนือจากการเหนี่ยวนำตัวเอง แต่ยังเนื่องจากขดลวดที่อยู่ใกล้เคียงในการเปลี่ยนแปลงปัจจุบันและการเหนี่ยวนำร่วมกัน

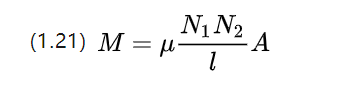
ค่าสัมประสิทธิ์การเหนี่ยวนำร่วมกันของวัสดุที่มีลักษณะเฉพาะเชิงเส้นจะประมาณได้จากสมการข้างต้น ซึ่งแสดงว่าค่าความเหนี่ยวนำร่วมกันได้รับผลกระทบจากจำนวนรอบของขดลวดทั้งสองในเวลาเดียวกัน

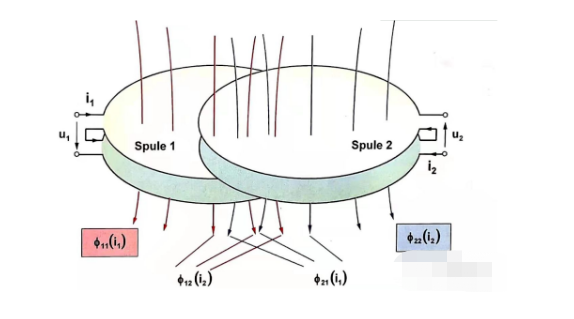
ละเว้นความต้านทานและตรวจสอบความเหนี่ยวนำของตัวเองและร่วมกันของขดลวดที่อยู่ติดกันสองตัว สมการแรงดันไฟฟ้าสามารถแสดงได้จากรูปที่ 1.5 เกี่ยวกับมอเตอร์กระแสตรง

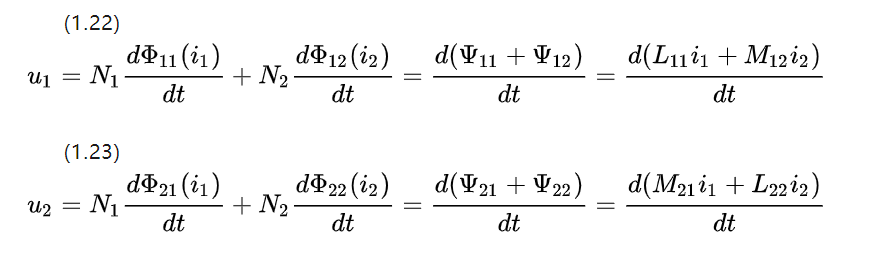
เนื่องจากชิ้นส่วนคัปปลิ้งมีพารามิเตอร์และรูปร่างของวัสดุเหมือนกัน ค่าสัมประสิทธิ์การเหนี่ยวนำร่วมที่ได้จึงเท่ากับ M12=M21

ดังนั้นขนาดของห่วงโซ่ข้อต่อบนขดลวดแต่ละอันจึงแปรผันตามความแรงของกระแสไฟฟ้าบนขดลวดของโรเตอร์ที่สอดคล้องกันสำหรับมอเตอร์กระแสตรง

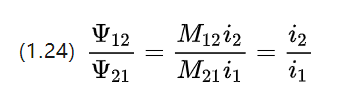
ทฤษฎีบท 1.5 โอห์มสำหรับพลังงานไฟฟ้าและวงจรแม่เหล็ก

ในโรงเรียนมัธยมศึกษา เราศึกษาทฤษฎีบทของโอห์ม ซึ่งระบุว่าความต้านทานของตัวนำคืออัตราส่วนของแรงดันและกระแสที่ปลายทั้งสองข้าง และมีสูตรที่อธิบายวัสดุต้านทานด้วย

Q ซึ่งเป็นค่าการนำไฟฟ้า ซึ่งเท่ากับส่วนกลับของค่าความต้านทาน P และอธิบายถึงความสามารถในการนำกระแส

นอกจากการใช้ความต้านทานแล้ว ยังสามารถอธิบายความสัมพันธ์ระหว่างแรงดันและกระแสไฟฟ้าได้โดยใช้รูปภาพการนำไฟฟ้าเมื่อมอเตอร์ไฟฟ้าทำงาน

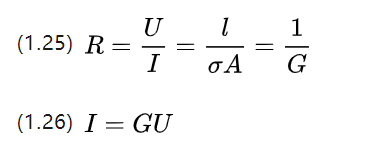
ตรวจสอบความเข้มกระแสต่อหน่วยพื้นที่ เช่น ความหนาแน่นกระแส J = I/A e (e คือเวกเตอร์หน่วย) โดยมีความหนาแน่นกระแสเป็นเวกเตอร์ที่ชี้ไปในทิศทางของกระแสสำหรับมอเตอร์ไฟฟ้ากระแสสลับ

สามารถรวมกับสมการแรงดันไฟฟ้า U=E.l และ (1.25) ที่เขียนใหม่ (1.26) เป็น

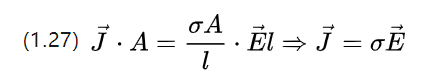
สมการข้างต้นอธิบายทฤษฎีบทของโอห์มในระดับจุลภาค เช่น การแปรผันของความหนาแน่นกระแสที่สอดคล้องกับความแรงของสนามคงที่ที่ใช้กับตัวนำ

Lm คือความยาวที่มีประสิทธิภาพของฟลักซ์แม่เหล็กผ่านส่วนของวงจรแม่เหล็ก และ A คือพื้นที่ฟลักซ์ที่สอดคล้องกัน

สมการข้างต้นคล้ายกับสูตรความต้านทาน

ให้เราเปลี่ยนรูปสูตรความต้านทานสนามแม่เหล็กอีกครั้ง และเราจะได้รับต่อไป

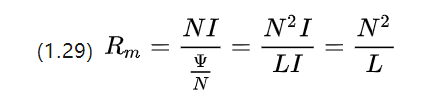
จะเห็นได้ว่าในหน่วยความต้านทานสนามแม่เหล็กนั้นตรงกันข้ามกับค่าสัมประสิทธิ์การเหนี่ยวนำ

ดำเนินการเปรียบเทียบกับแนวคิดของสื่อนำไฟฟ้าต่อไป เราได้รับสื่อนำไฟฟ้า A (magnetische Leitwert ใน [H] หรือ [Ωs])

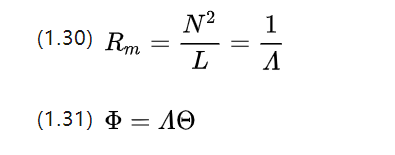
ในวงจรเราพบองค์ประกอบดิฟเฟอเรนเชียลสำหรับ (1.26) และรับทฤษฎีบทของโอห์มด้วยกล้องจุลทรรศน์ แล้วทฤษฎีบทของโอห์มด้วยกล้องจุลทรรศน์ที่สอดคล้องกับวงจรแม่เหล็กคืออะไร?

เราสามารถเขียนสมการใหม่ (1.31) ได้โดยสังเกตว่าฟลักซ์แม่เหล็กนั้นมีความหนาแน่นของฟลักซ์ B ซึ่งให้ผล

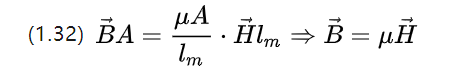
ดังนั้นทฤษฎีบทของวงจรแม่เหล็กด้วยกล้องจุลทรรศน์คือสมการ (1.10) และความแรงของสนามแม่เหล็กด้านล่างคือความหนาแน่นของฟลักซ์ที่ได้จากการทำให้เป็นแม่เหล็กของสนามแม่เหล็กคงที่

การวิเคราะห์เชิงคำนวณของความไม่เต็มใจสามารถใช้เพื่อรับรู้การวิเคราะห์องค์ประกอบระดับจุลภาคของฟลักซ์ในขดลวดมอเตอร์ทั้งหมด ส่วนหลัก และส่วนช่องว่างอากาศระหว่างกลาง ซึ่งสามารถรับรู้การวิเคราะห์องค์ประกอบไฟไนต์แบบแยกส่วน FEM (Finite-Elemente-Methode) ของวงจรแม่เหล็กทั้งหมด

นอกจากนี้ยังเป็นไปได้ที่จะใช้ทฤษฎีบทของ Kirchhoff กับวงจรในวงจรแม่เหล็กซึ่งใช้งานง่ายและสะดวกมาก

ยินดีต้อนรับสู่แบ่งปันข้อมูลเพิ่มเติมเกี่ยวกับมอเตอร์ไฟฟ้าในพื้นที่แสดงความคิดเห็น!

หากมีข้อสงสัยเกี่ยวกับมอเตอร์ไฟฟ้า โปรดติดต่อช่างไฟฟ้ามืออาชีพ ผู้ผลิต ใน จีน ดังนี้