1. Физический принцип работы электродвигателя
1.1 Maxwell's system of equations
Электродвигатель представляет собой преобразователь, который постоянно преобразует электромагнитную энергию и механическую энергию.
Когда подается электрическая энергия, электродвигатель может непрерывно выдавать крутящий момент и механическую энергию.
то есть электродвигатель; и наоборот, если внешняя сила постоянно толкает вал электродвигателя и вводит механическую энергию, электродвигатель может непрерывно выдавать напряжение и электрическую энергию от конца провода в обратном направлении, то есть от генератора.
Исторически статический трансформатор также считался электродвигателем, но постепенно он стал относиться исключительно к электродвигателям и генераторам.
Одним из преимуществ электродвигателей является то, что их потери относительно малы, благодаря чему достигается высокий КПД.
Большие электродвигатели могут достигать КПД до 99%.

When talking about electromagnetic systems, Maxwell's system of equations is inevitable.
В макроскопическом мире и даже в микроскопическом мире
Maxwell's system of equations can be used very effectively to describe the system properties.
Maxwell's system of equations has been summarized from previous studies of electromagnetic phenomena.
Есть четыре основных уравнения, как в дифференциальной, так и в интегральной форме.
Now let's examine Maxwell's system of equations in integral form.
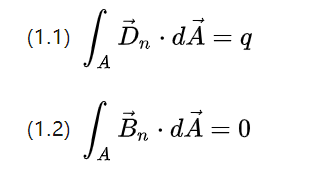
Приведенные выше два уравнения описывают поток плотности поля, соответственно, суммарную картину сдвига потенциала истечения и суммарную картину индукции вращающегося магнитного поля на поверхности замкнутого пространства.
Согласно знаниям, полученным в средней школе, электрическое поле может быть создано путем возбуждения точечного заряда, магнитное поле может быть возбуждено не магнитным монополем, а для расширения закрытого пути, поэтому электрическое поле активно, магнитное поле пассивный.
Таким образом, общий поток сдвига потенциала равен общему заряду q, а полный магнитный поток равен 0.
Приведенные выше два уравнения описывают спиновые величины напряженности поля, интегралы полной напряженности электрического поля и полной напряженности магнитного поля.
Соответствующая скорости изменения магнитного потока и скорости изменения сдвига потенциала (силы тока) соответственно за один оборот по пути кривой на замкнутом пространстве кривой.
Формулы Гаусса и Стокса также позволяют переписать приведенные выше четыре уравнения в дифференциальную форму следующим образом.
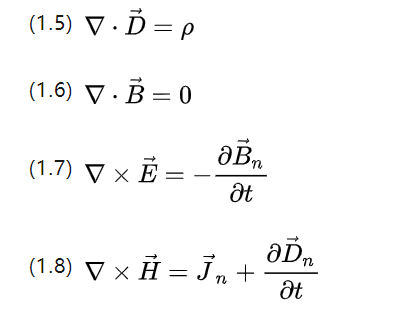
▽ для оператора Набла, с векторным скалярным произведением для расчета разброса и вилочным произведением для расчета спина, P для плотности тела заряда и Jn для плотности тока.
Приведенные выше уравнения могут описать в основном все электромагнитное поведение, которое происходит во всех системах асинхронных двигателей переменного тока.
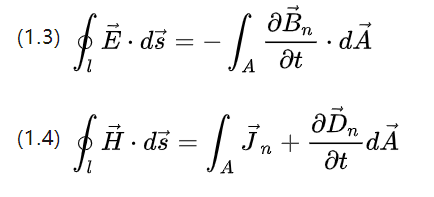
1.2 Материальная поляризация и намагниченность для электрической энергии
В приложенном электрическом вращающемся магнитном поле молекулы материала изменят свою ориентацию, поскольку на полярность влияет напряженность поля.
Электрические домены, образованные исходными неравномерно расположенными молекулярными группами различных размеров, будут поляризованы из-за приложенного магнитного поля, и ориентация распределения заряда сходится.
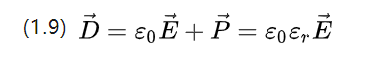
E0=8,854187817*10-12Ф/м — диэлектрическая проницаемость вакуума, которая также является диэлектрической проницаемостью вакуума, а P — относительная диэлектрическая проницаемость, которая определяется свойствами самого материала.
(1.9) вместе описывает плотность сдвига потенциала приложенного электрического поля и соответствующую картину интенсивности поляризации.
В приложенном магнитном поле соответствующие магнитные домены и силы намагниченности могут быть получены таким же образом.
В отличие от электрического поля вводится сила магнитной поляризации M, которая описывает разницу между силой магнитной индукции материала и вакуумной среды.
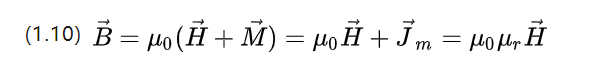
U0=4π*10-7 N.A-2 — проницаемость вакуума, а Ur — относительная проницаемость, которая описывает способность материала пропускать магнитное поле.
Если Ур<=1 антимагнитен, материал препятствует прохождению магнитного поля; если изображение парамагнитно, материал подчиняется прохождению магнитного поля.
Если Ур>=1o 5 является ферромагнитным, такой материал, как феррокобальтовый никель, будет усиливать магнитное поле после намагничивания. А затем сохранить определенную силу магнитного поля после удаления магнитного поля, что называется остаточным магнетизмом.
В процессе работы двигателя будет происходить постоянное намагничивание и размагничивание, поэтому следует также уделить внимание изучению линий гистерезиса различных материалов.
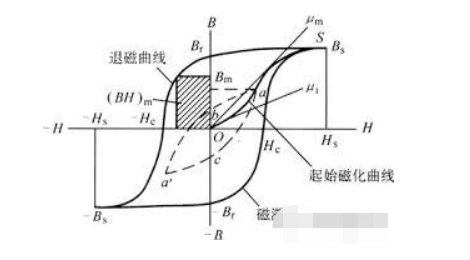
Линия гистерезиса описывает увеличение магнитной индукции магнитного материала по мере увеличения напряженности поля под действием приложенного магнитного поля напряженностью H.
Эта магнитная индукция не следует за напряженностью поля после достижения магнитного насыщения.
После достижения магнитного насыщения трудно проследить увеличение напряженности поля. Когда напряженность внешнего магнитного поля медленно уменьшается до нуля, видно, что кривая размагничивания все еще сохраняет остаточную намагниченность B, когда проходит нулевую точку.
Эта остаточная намагниченность показывает общий принцип изготовления постоянных магнитов, то есть направленное намагничивание с последующим постепенным размагничиванием. При приложении обратного магнитного поля сила магнитной индукции стремится к нулю или даже увеличивается в обратном направлении, и это превышение называется коэрцитивной силой Н.
1.3 Электромагнитная сила и механическая энергия
Наибольшая ценность двигателя состоит в том, чтобы реализовать преобразование электрической энергии в механическую, совершать внешнюю работу и совершать целевое движение.
Движение заряженной частицы в магнитном поле подчинено перпендикулярной к направлению движения силе Лоренца, макроскопическим выражением которой является сила Ампера Hm = Il * B , о которой можно судить, используя правило левой руки для определения направление,
I — эффективная длина проводника в магнитном поле в направлении тока.
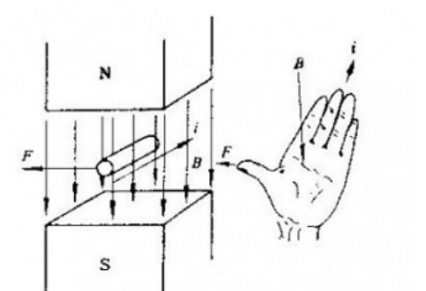
Существует также соответствующая сила электрического поля в электростатическом поле Fe=qE.
И магнитное, и электрическое поля сами по себе являются полями, и сила, приложенная к элементу заряда или тока в них, зависит от объема и плотности поля, и, таким образом, соответствующую силу поля можно рассматривать в терминах поля.
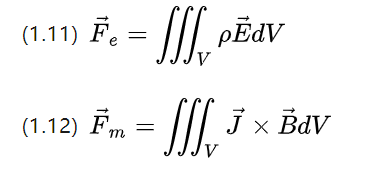
Приведенные выше два уравнения по-прежнему сохраняют симметрию: плотность заряда P в определенном объеме из-за напряженности поля электрического поля создает плотность электрической силы fe = pE,
Плотность тока J в определенном объеме за счет напряженности магнитного поля дает плотность магнитной силы Fm = J * B (приведенное выше уравнение (1.12) необходимо использовать в случае изотропных материалов и постоянного тока).
Это выражение вдохновляет нас непосредственно исследовать энергию и плотность энергии электромагнитного поля.
Таким образом, потенциальную электромагнитную энергию в определенной точке можно определить, найдя градиент, чтобы получить соответствующую плотность электромагнитной силы и, таким образом, найти полную электромагнитную силу, действующую на исследуемый объект.
1.4 Модель катушки
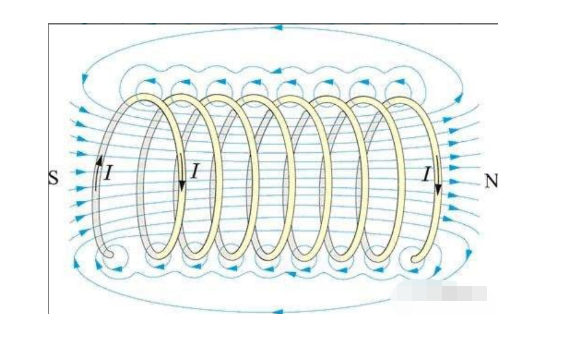
Катушка является фундаментальным элементом, который образует модель асинхронных двигателей, соединяя схемную модель двигателя переменного тока и физическую модель объекта.
Прямой участок проводника под напряжением создает вокруг себя тороидальное магнитное поле (согласно уравнению 1.4).
Когда проводник замкнут в начале и конце, тороидальное поле образует магнитные силовые линии в центре кольца проводника, которые проходят вертикально через кольцо проводника, например соленоид.
Принимая во внимание только ток в проводнике под напряжением, (1.4) упрощается до:
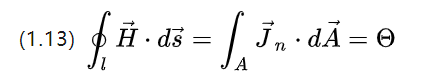
Магнитодвижущая сила (magnetische Durchfluchtung), являющаяся источником напряженности поля возбуждения, представляет собой, по существу, силу полного тока, проходящего через сечение замкнутого проводника в [А].
Поскольку на практике проволока под напряжением будет смотана в катушку, ток в проволоке дискретизируется и (1.13) переписывается в виде
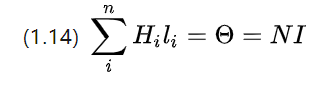
N - общее количество витков в катушке, т. е. число витков.
Видно, что чем больше число витков, тем выше общий ток, выше магнитный потенциал и тем сильнее может быть возбуждено магнитное поле.
Одновитковая катушка в изменяющемся во времени магнитном поле будет индуцировать напряжение на обоих концах провода, явление, описываемое формулой (1.3).
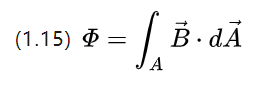
Можно понять, что магнитную индукцию можно интерпретировать и как плотность магнитного потока, которую можно получить, подставив (1.3)
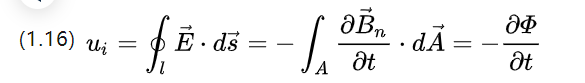
Ui - наведенный электрический потенциал, рассмотрим две формы изменения потока, одна из которых заключается в изменении площади катушки, но изменении плотности потока, тогда есть следующие;
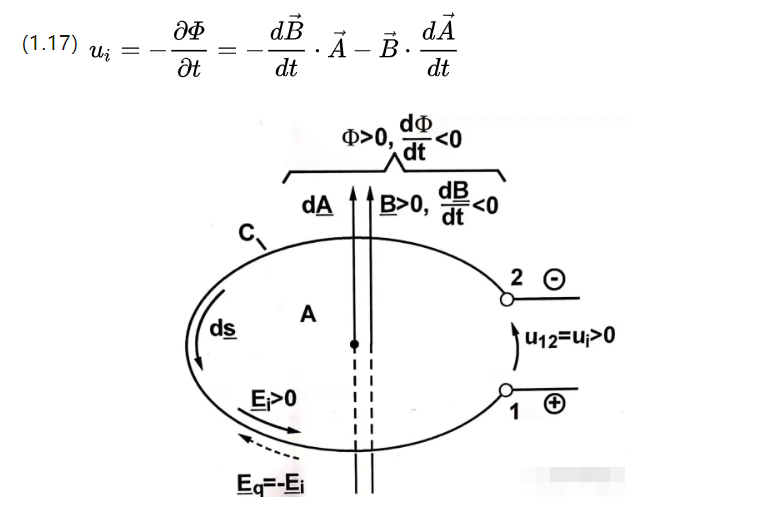
Первая часть представляет собой формально преобразованный индукционный потенциал, а вторая часть представляет собой трансляционно преобразованный индукционный потенциал.
Первый имеет изменяющуюся во времени плотность магнитного потока, а второй имеет изменяющуюся во времени эффективную площадь катушки.
Этот принцип индукции упоминается в школьной физике и также известен как теорема флейты.
Когда катушка имеет много витков, общий эффективный поток в точности равен целому числу витков расширенной катушки, что вводит понятие магнитной цепи.
Цепочка показана на рисунке ниже.
Обратите внимание, что магнитная цепь является скалярной величиной, как и магнитный поток. Поскольку изменение тока само по себе может также вызвать изменение потока, тенденция состоит в том, чтобы препятствовать изменению потока, которое можно определить как:
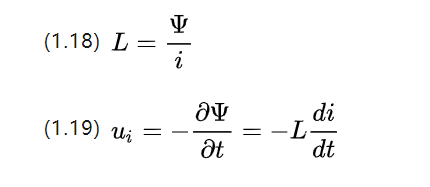
i — переменная сила тока, L — коэффициент собственной индуктивности в Генри [H], а его величина связана с формой объема катушки, числом витков и магнитной проницаемостью.
Катушки в асинхронных двигателях изготавливаются из ферромагнитного материала в середине катушки, такого как железный сердечник, для увеличения магнитной проницаемости, так что катушка наматывается на железный сердечник, отсюда и название обмотки.
Для сечения линейно-однородного материала его коэффициент собственной индуктивности можно аппроксимировать следующим уравнением
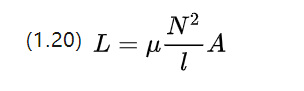
Самоиндукция - это катушка собственных изменений тока, вызывающая явление подавления напряжения, ее тенденция препятствовать изменениям тока в электродвигателе постоянного тока.
Когда две катушки расположены близко друг к другу, в дополнение к их собственной индуктивности, но также из-за соседних катушек по изменению тока и взаимной индуктивности
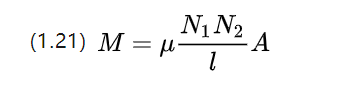
Коэффициент взаимной индуктивности материалов с линейными тождествами аппроксимируется приведенным выше уравнением, которое показывает, что на взаимную индуктивность влияет количество витков двух катушек одновременно.
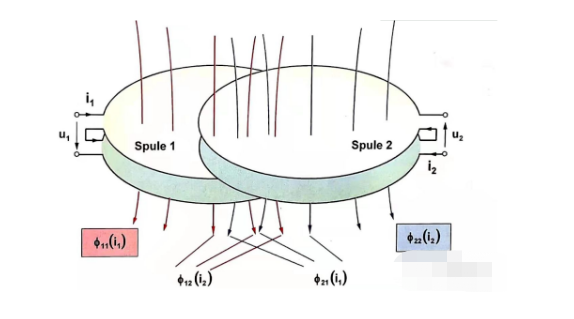
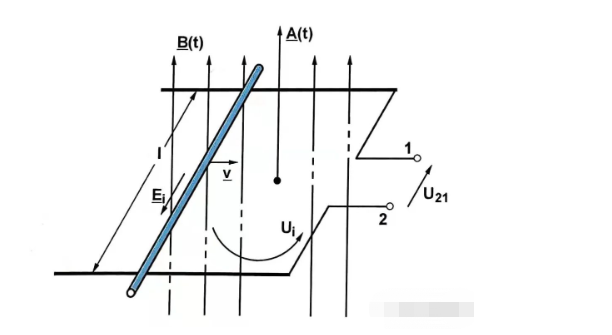
Пренебрегая сопротивлением и исследуя собственную и взаимную индуктивность двух соседних катушек, уравнение напряжения можно вывести из рисунка 1.5 для двигателей постоянного тока.
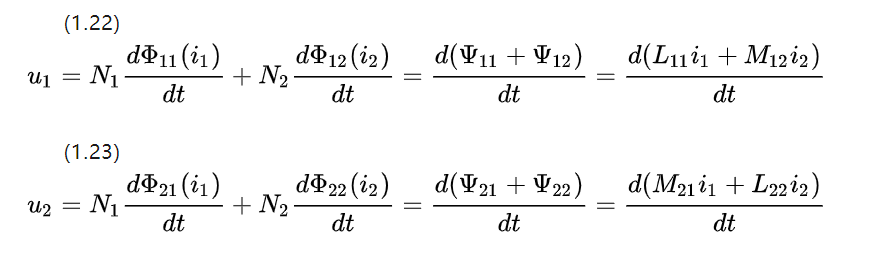
Поскольку детали муфты имеют одинаковые параметры материала и форму, результирующие коэффициенты взаимной индуктивности равны М12=М21.
Таким образом, размер цепей связи на каждой катушке пропорционален силе тока на соответствующей катушке обмоток ротора для двигателя постоянного тока.
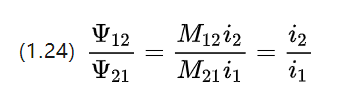
1.5 Ohm's theorem for electrical energy and magnetic circuits
In secondary school we studied Ohm's theorem, which states that the resistance of a conductor is the ratio of the voltage and current at both ends, and that there is a formula to describe the resistive material itself.
Q, который является проводимостью, которая в точности обратна удельному сопротивлению P и описывает способность проводить ток.
В дополнение к приложенному сопротивлению, связь между напряжением и током также может быть описана с помощью картины проводимости при работе электродвигателя.
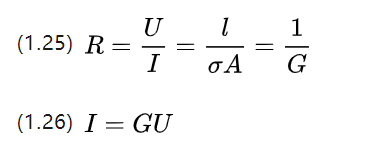
Теперь изучите силу тока на единицу площади, т. е. плотность тока J = I/A e (e — единичный вектор), с плотностью тока в виде вектора, указывающего в направлении тока для двигателей переменного тока.
Это можно объединить с уравнением напряжения U=E.l и (1.25) переписать (1.26) в виде
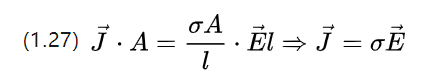
The above equation describes the Ohm's theorem at the microscopic level, i.e., the variation of the current density corresponding to a constant field strength applied to the conductor.
Lm — эффективная длина магнитного потока через сечение магнитопровода, A — соответствующая площадь потока.
Приведенное выше уравнение очень похоже на формулу сопротивления.
Снова деформируем формулу магнитосопротивления, и мы можем продолжить получать
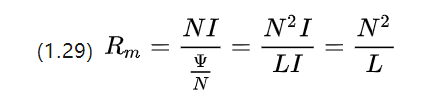
Можно видеть, что в единицах магнитосопротивление на самом деле является обратной величиной коэффициента индуктивности.
Продолжая аналогию с понятием проводимости, мы получаем магнитную проводимость A (magnetische Leitwert, в [Гн] или [Ом])
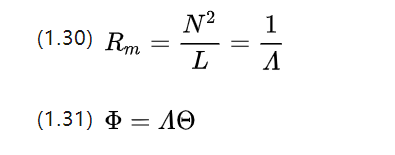
In the circuit we find the differential elements for (1.26) and get the microscopic Ohm's theorem, so what is the microscopic Ohm's theorem corresponding to the magnetic circuit?
Мы можем переписать уравнение (1.31), отметив, что магнитный поток сам по себе имеет плотность потока B, что дает тогда
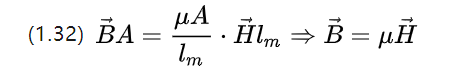
So the microscopic magnetic circuit Ohm's theorem is equation (1.10), and the magnetic field strength under is the flux density obtained from the magnetization of a constant magnetic field.
Вычислительный анализ сопротивления может быть использован для проведения анализа микроэлементов потока во всем полюсе обмотки двигателя, в части сердечника и в части промежуточного воздушного зазора, который может реализовать дискретный анализ методом конечных элементов FEM (метод конечных элементов). всей магнитной цепи.
It is also possible to apply Kirchhoff's theorem for the circuit in the magnetic circuit, which is very intuitive and convenient.
Добро пожаловать, чтобы поделиться с нами дополнительной информацией об электродвигателях в комментариях!
Любой запрос об электродвигателе, пожалуйста, свяжитесь с профессиональным электродвигателем. производитель в Китай следующее:

Dongchun Motor предлагает широкий ассортимент электродвигателей, которые используются в различных отраслях, таких как транспорт, инфраструктура и строительство.
Получите оперативный ответ.








