1. O princípio físico do trabalho do motor elétrico
1.1 Maxwell's system of equations
O motor elétrico é um transdutor que converte constantemente energia eletromagnética e energia mecânica.
Quando a energia elétrica é inserida, o motor elétrico pode produzir continuamente torque e energia mecânica.
ou seja, o motor elétrico; inversamente, se uma força externa continuamente empurra o eixo do motor elétrico e insere energia mecânica, o motor elétrico pode continuamente produzir tensão e energia elétrica da extremidade do fio ao contrário, ou seja, o gerador.
Historicamente, o transformador estático também era considerado um motor elétrico, mas gradualmente evoluiu para se referir exclusivamente a motores e geradores elétricos.
Uma das vantagens dos motores elétricos é que suas perdas são relativamente pequenas, por isso alcançam alta eficiência.
Grandes motores elétricos podem atingir eficiências de até 99%.

When talking about electromagnetic systems, Maxwell's system of equations is inevitable.
No mundo macroscópico e mesmo no mundo microscópico,
Maxwell's system of equations can be used very effectively to describe the system properties.
Maxwell's system of equations has been summarized from previous studies of electromagnetic phenomena.
Existem quatro equações muito básicas, tanto na forma diferencial quanto na integral.
Now let's examine Maxwell's system of equations in integral form.
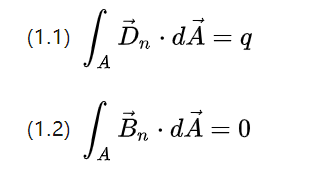
As duas equações acima descrevem o fluxo da densidade de campo, respectivamente, o total da imagem de deslocamento do potencial de saída e o total da imagem de indução do campo magnético rotativo em uma superfície de espaço fechado
De acordo com o conhecimento aprendido no ensino médio, o campo elétrico pode ser gerado por excitação de carga pontual, o campo magnético não pode ser excitado pelo monopolo magnético, mas sim estender o caminho fechado, então o campo elétrico está ativo, o campo magnético é passiva.
Assim, o fluxo de deslocamento potencial total é a carga total q e o fluxo magnético total é 0.
As duas equações acima descrevem as quantidades de spin da intensidade do campo, as integrais da intensidade total do campo elétrico e a intensidade total do campo magnético.
Correspondente à taxa de variação do fluxo magnético e à taxa de variação do deslocamento de potencial (intensidade da corrente), respectivamente, para uma volta ao longo do caminho da curva em uma curva de espaço fechado.
As fórmulas de Gauss e Stokes também permitem a reescrita das quatro equações acima na forma diferencial, como segue.
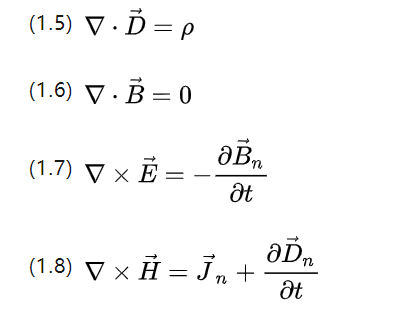
▽ para o operador Nabla, com produto vetorial vetorial para calcular a dispersão e produto bifurcado para calcular o spin, P para a densidade do corpo de carga e Jn para a densidade de corrente.
As equações acima podem descrever basicamente todo o comportamento eletromagnético que ocorre em todos os sistemas de motores de indução CA.
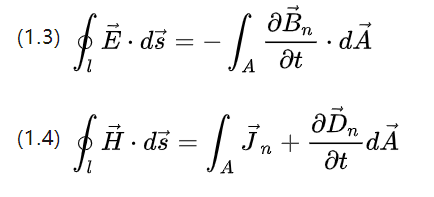
1.2 Polarização e magnetização de materiais para energia elétrica
Em um campo magnético rotativo elétrico aplicado, as moléculas do material mudarão sua orientação porque a polaridade é afetada pela intensidade do campo.
Os domínios elétricos formados pelos grupos moleculares originais arranjados desigualmente de vários tamanhos serão polarizados por causa do campo magnético aplicado, e a orientação da distribuição de carga converge.
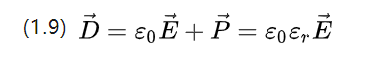
E0=8,854187817*10-12F/m é a permissividade do vácuo, que também é a constante dielétrica do vácuo, e P é a constante dielétrica relativa, que é determinada pelas propriedades do próprio material.
(1.9) descreve a densidade de deslocamento de potencial do campo elétrico aplicado e a imagem de intensidade de polarização correspondente juntos.
Em um campo magnético aplicado, os domínios magnéticos correspondentes e as forças de magnetização podem ser obtidos da mesma maneira.
Ao contrário do campo elétrico, é introduzida uma força de polarização magnética M, que descreve a diferença entre a força de indução magnética do material e a do ambiente de vácuo.
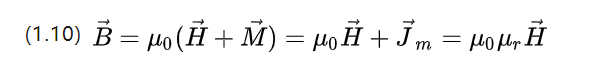
U0=4π*10-7 N.A-2 é a permeabilidade ao vácuo e Ur é a permeabilidade relativa, que descreve a capacidade do material de permitir a passagem de um campo magnético.
Se você<=1 é antimagnético, o material impede a passagem de um campo magnético; se a imagem for paramagnética, o material obedece à passagem de um campo magnético.
Se você>=1o 5 é ferromagnético, o material como ferro-cobalto níquel aumentará o campo magnético após a magnetização. E então retém uma certa força do campo magnético após remover o campo magnético, que é chamado de magnetismo remanescente.
No processo de operação do motor haverá constante magnetização e desmagnetização, portanto, atenção também deve ser dada ao exame das linhas de histerese de diferentes materiais.
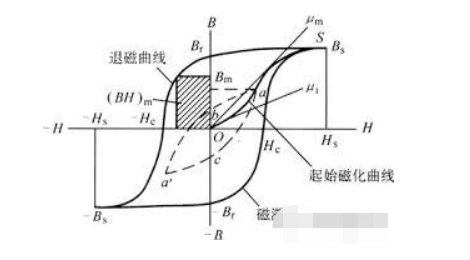
A linha de histerese descreve a indução magnética crescente de um material magnético à medida que a intensidade do campo aumenta sob a ação de um campo magnético aplicado de intensidade H.
Esta indução magnética não segue a intensidade do campo após atingir a saturação magnética.
Depois que a saturação magnética é atingida, é difícil acompanhar o aumento da intensidade do campo. Quando a força do campo magnético externo diminui lentamente para zero, pode-se ver que a curva de desmagnetização ainda retém a magnetização remanescente B quando passa do ponto zero.
Esta magnetização remanescente mostra o princípio geral de fabricação de ímãs permanentes, ou seja, magnetização direcional seguida de desmagnetização gradual. Quando o campo magnético inverso é aplicado, a força da indução magnética vai a zero ou até aumenta na direção oposta, e esse excesso é chamado de coercividade H.
1.3 Força eletromagnética e energia mecânica
O maior valor do motor é realizar a conversão de energia elétrica em energia mecânica, realizar trabalho externamente e executar o movimento alvo.
O movimento de uma partícula carregada em um campo magnético está sujeito à força de Lorentz perpendicular à direção do movimento, cuja expressão macroscópica é a força Ampere Hm = Il * B , que pode ser julgada usando a regra da mão esquerda para determinar o direção,
I é o comprimento efetivo do condutor no campo magnético na direção da corrente.
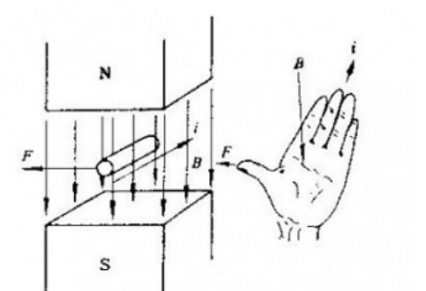
Há também uma força de campo elétrico correspondente no campo eletrostático Fe=qE .
E os campos magnético e elétrico são eles próprios campos, e a força aplicada à carga ou elemento atual neles depende do volume e da densidade do campo e, portanto, a força de campo correspondente pode ser examinada em termos do campo.
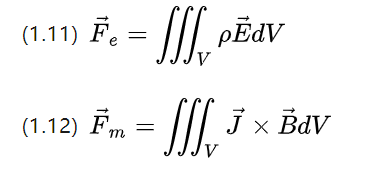
As duas equações acima ainda mantêm a simetria, a densidade de carga P em um determinado volume devido à intensidade do campo do campo elétrico produz a densidade de força elétrica fe = pE,
A densidade de corrente J em um determinado volume devido à intensidade do campo magnético produz a densidade de força magnética Fm = J * B (a equação acima (1.12) deve ser usada no caso de materiais isotrópicos e de corrente constante).
Essa expressão nos inspira a examinar diretamente a energia e a densidade de energia do campo eletromagnético.
Desta forma, a energia potencial eletromagnética em um determinado ponto pode ser determinada encontrando o gradiente para obter a densidade de força eletromagnética correspondente e, assim, encontrar a força eletromagnética total sobre o objeto sob investigação.
1.4 Modelo da bobina
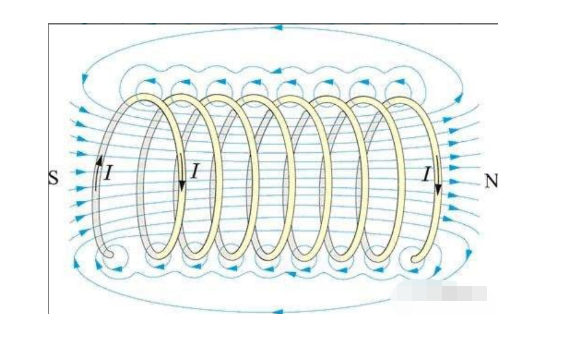
Uma bobina é um elemento fundamental que forma um modelo de motores de indução, fazendo a ponte entre o modelo de circuito do motor de corrente alternada e o modelo físico do objeto.
Uma seção reta de condutor energizado gera um campo magnético toroidal ao seu redor (conforme a equação 1.4).
Quando o condutor é fechado no início e no fim, o campo toroidal forma linhas magnéticas de força no centro do anel condutor que passam verticalmente pelo anel condutor, como um solenóide.
Considerando apenas a corrente no condutor energizado, (1.4) simplifica para:
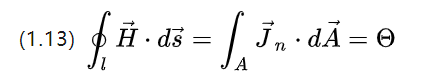
A força magnetomotriz (magnetische Durchfluchtung), que é a fonte da intensidade do campo de excitação, é essencialmente a intensidade da corrente total que passa por uma seção de condutor fechado em [A].
Como na prática o fio energizado será enrolado em uma bobina, a corrente do fio é discretizada e (1.13) é reescrita como
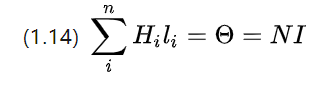
N é o número total de enrolamentos na bobina, ou seja, o número de voltas.
Pode-se ver que, se o número de voltas for maior, a corrente total é maior, o potencial magnético é maior e mais forte o campo magnético pode ser excitado.
Uma bobina de volta única em um campo magnético variável no tempo induzirá uma tensão em ambas as extremidades do fio, um fenômeno descrito por (1.3).
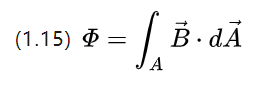
Pode-se entender que a indução magnética também pode ser interpretada como a densidade do fluxo magnético, que pode ser obtida substituindo (1.3)
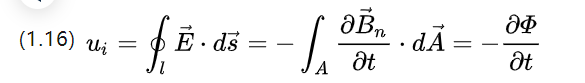
Ui é o potencial elétrico induzido, considere duas formas de mudança de fluxo, uma é mudar a área da bobina, mas mudar a densidade de fluxo, então existem as seguintes;
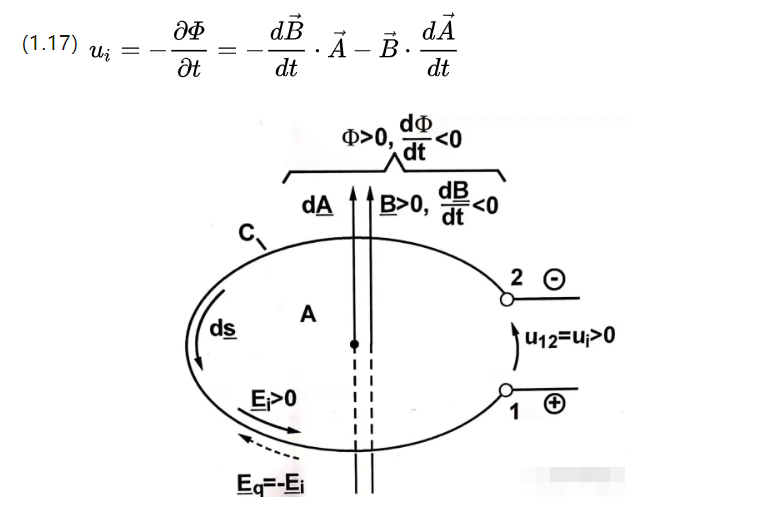
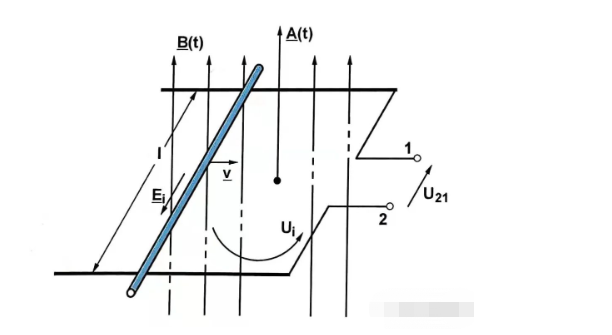
A primeira parte é o potencial de indução formalmente transformado e a última parte é o potencial de indução translacionalmente transformado.
O primeiro tem uma densidade de fluxo magnético variável no tempo, enquanto o último tem uma área de bobina efetiva variável no tempo.
Esse princípio de indução é mencionado na física do ensino médio e também é conhecido como o teorema da flauta.
Quando uma bobina tem muitas voltas, o fluxo efetivo total é exatamente um múltiplo inteiro das voltas da bobina expandida, introduzindo assim o conceito de uma cadeia magnética.
A cadeia é definida na figura abaixo.
Observe que a cadeia magnética é uma quantidade escalar, assim como o fluxo magnético. Como uma mudança na própria corrente também pode causar uma mudança no fluxo, a tendência é impedir a mudança no fluxo, que pode ser definida como:
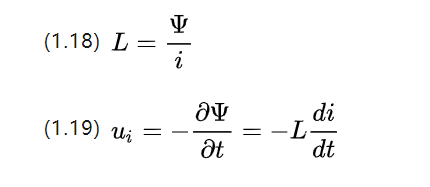
i é a variação da intensidade da corrente, L é o coeficiente de auto-indutância em Henry [H], e seu tamanho está relacionado com a forma do volume da bobina, número de voltas e permeabilidade magnética.
As bobinas dos motores de indução são feitas para ter material ferromagnético no meio da bobina, como um núcleo de ferro, para aumentar a permeabilidade magnética, de modo que a bobina seja enrolada no núcleo de ferro, daí o nome enrolamento.
Para uma seção de material linearmente homogêneo, seu coeficiente de auto-indutância pode ser aproximado pela seguinte equação
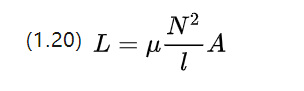
A auto-indutância é uma bobina de suas próprias mudanças de corrente para induzir o fenômeno da tensão de supressão, sua tendência de impedir mudanças de corrente sobre o motor elétrico dc.
Quando duas bobinas próximas uma da outra, além de sua própria indutância, mas também por causa das bobinas vizinhas nas mudanças de corrente e indutância mútua
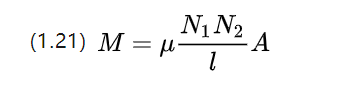
O coeficiente de indutância mútua de materiais com identidades lineares é aproximado pela equação acima, que mostra que a indutância mútua é afetada pelo número de voltas das duas bobinas ao mesmo tempo.
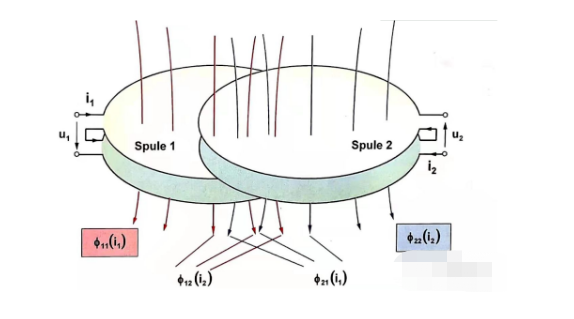
Ignorando a resistência e examinando a indutância própria e mútua das duas bobinas adjacentes, a equação de tensão pode ser listada na Figura 1.5 sobre motores CC
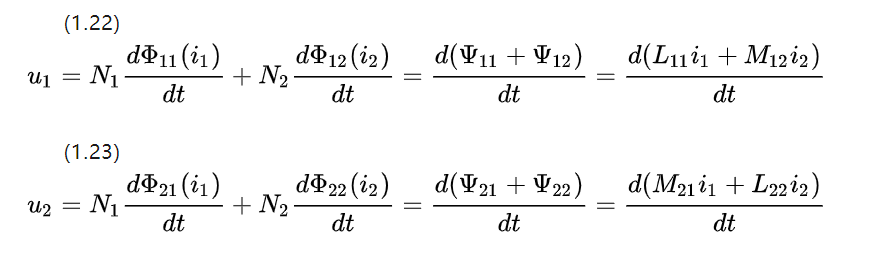
Como as partes do acoplamento têm os mesmos parâmetros de material e formato, os coeficientes de indutância mútua resultantes são iguais M12=M21.
Portanto, o tamanho das correntes de acoplamento em cada bobina é proporcional à intensidade da corrente na bobina dos enrolamentos do rotor correspondente para o motor CC.
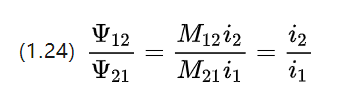
1.5 Ohm's theorem for electrical energy and magnetic circuits
In secondary school we studied Ohm's theorem, which states that the resistance of a conductor is the ratio of the voltage and current at both ends, and that there is a formula to describe the resistive material itself.
Q, que é a condutividade, que é exatamente o recíproco da resistividade P e descreve a capacidade de conduzir corrente.
Além de aplicar resistência, a relação entre tensão e corrente também pode ser descrita usando a imagem da condutividade quando o motor elétrico funciona.
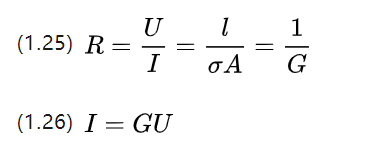
Agora examine a intensidade de corrente por unidade de área, ou seja, densidade de corrente J = I/A e (e é o vetor unitário), com a densidade de corrente como um vetor apontando na direção da corrente para motores CA.
Isso pode ser combinado com a equação de tensão U=E.l e (1.25) reescrita (1.26) como
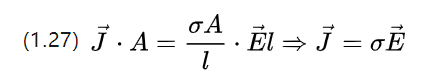
The above equation describes the Ohm's theorem at the microscopic level, i.e., the variation of the current density corresponding to a constant field strength applied to the conductor.
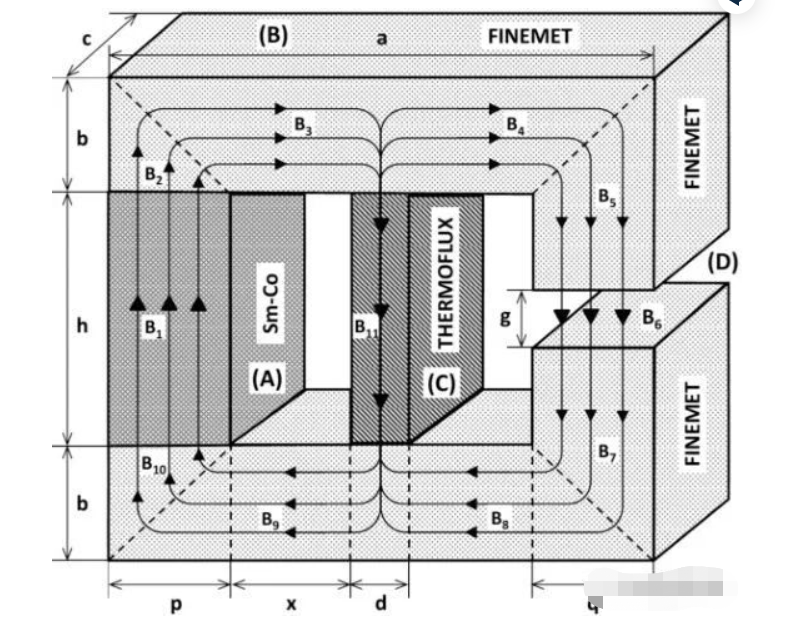
Lm é o comprimento efetivo do fluxo magnético através de uma seção do circuito magnético e A é a área de fluxo correspondente.
A equação acima é muito semelhante à fórmula de resistência.
Vamos deformar a fórmula de magnetorresistência novamente e podemos continuar a obter
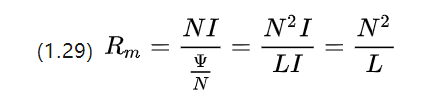
Pode-se ver que em unidades a magnetorresistência é na verdade o inverso do coeficiente de indutância.
Continuando a analogia com o conceito de condutância, obtemos a condutância magnética A (magnetische Leitwert, em [H] ou [Ωs])
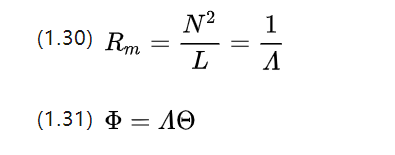
In the circuit we find the differential elements for (1.26) and get the microscopic Ohm's theorem, so what is the microscopic Ohm's theorem corresponding to the magnetic circuit?
Podemos reescrever a equação (1.31), observando que o próprio fluxo magnético tem uma densidade de fluxo B , que então produz
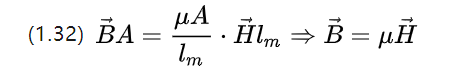
So the microscopic magnetic circuit Ohm's theorem is equation (1.10), and the magnetic field strength under is the flux density obtained from the magnetization of a constant magnetic field.
A análise computacional da relutância pode ser usada para realizar uma análise de microelementos do fluxo em todo o pólo do enrolamento do motor, parte do núcleo e parte intermediária do entreferro, que pode realizar uma análise de elementos finitos discretos FEM (Finite-Elemente-Methode) de todo o circuito magnético.
It is also possible to apply Kirchhoff's theorem for the circuit in the magnetic circuit, which is very intuitive and convenient.
Bem-vindo a compartilhar conosco mais informações sobre motores elétricos na área de comentários!
Qualquer dúvida sobre motor elétrico, entre em contato com o motor elétrico profissional fabricante em China do seguinte modo:

A Dongchun motor possui uma ampla gama de motores elétricos que são usados em vários setores, como transporte, infraestrutura e construção.
Obtenha uma resposta imediata.








