လျှပ်စစ်မော်တာများ၏ရုပ်ပိုင်းဆိုင်ရာအခြေခံ

1. လျှပ်စစ်မော်တာ၏ရုပ်ပိုင်းဆိုင်ရာနိယာမ

1.1 Maxwell ၏ ညီမျှခြင်းစနစ်

လျှပ်စစ်မော်တာသည် လျှပ်စစ်သံလိုက်စွမ်းအင်နှင့် စက်စွမ်းအင်ကို အဆက်မပြတ်ပြောင်းလဲပေးသော transducer တစ်ခုဖြစ်သည်။

လျှပ်စစ်စွမ်းအင်ကို ထည့်သွင်းသည့်အခါ လျှပ်စစ်မော်တာသည် torque နှင့် စက်စွမ်းအင်ကို အဆက်မပြတ်ထုတ်ပေးနိုင်သည်။

ဥပမာအားဖြင့်၊ လျှပ်စစ်မော်တာ; ဆန့်ကျင်ဘက်အားဖြင့်၊ ပြင်ပမှတွန်းအားတစ်ခုသည် လျှပ်စစ်မော်တာရိုးတံကို အဆက်မပြတ်တွန်းအားပေးပြီး စက်ပိုင်းဆိုင်ရာစွမ်းအင်ကို ထည့်သွင်းပါက၊ လျှပ်စစ်မော်တာသည် ဝါယာကြိုးအဆုံးမှ လျှပ်စစ်စွမ်းအင်ကို ပြောင်းပြန်ဖြင့် အဆက်မပြတ်ထုတ်ပေးနိုင်သည်၊ ဆိုလိုသည်မှာ ဂျင်နရေတာဖြစ်သည်။

သမိုင်းကြောင်းအရ၊ static transformer ကို လျှပ်စစ်မော်တာအဖြစ်လည်း ရေတွက်ခဲ့ကြသော်လည်း၊ လျှပ်စစ်မော်တာများနှင့် ဂျင်နရေတာများကို သီးသန့်ရည်ညွှန်းရန် တဖြည်းဖြည်း ပြောင်းလဲလာသည်။

လျှပ်စစ်မော်တာများ၏ အားသာချက်များထဲမှ တစ်ခုမှာ ၎င်းတို့၏ ဆုံးရှုံးမှုသည် သေးငယ်သောကြောင့် စွမ်းဆောင်ရည် မြင့်မားသည်။

ကြီးမားသောလျှပ်စစ်မော်တာများသည် 99% ထိထိရောက်မှုရရှိနိုင်ပါသည်။

လျှပ်စစ်သံလိုက်စနစ်များအကြောင်းပြောသောအခါ Maxwell ၏ညီမျှခြင်းစနစ်သည် ရှောင်လွှဲ၍မရပါ။

မက်ခရိုစကုပ်ကမ္ဘာနှင့် အဏုကြည့်ကမ္ဘာတွင်ပင်၊

Maxwell ၏ ညီမျှခြင်းစနစ်သည် စနစ်ဂုဏ်သတ္တိများကိုဖော်ပြရန် အလွန်ထိရောက်စွာအသုံးပြုနိုင်ပါသည်။

Maxwell ၏ ညီမျှခြင်းစနစ်အား လျှပ်စစ်သံလိုက်ဖြစ်စဉ်များ၏ ယခင်လေ့လာမှုများမှ အကျဉ်းချုံးထားသည်။

ကွဲပြားမှုနှင့် ပေါင်းစပ်ပုံစံနှစ်မျိုးလုံးတွင် အလွန်အခြေခံညီမျှခြင်း လေးခုရှိသည်။

ယခု Maxwell ၏ ညီမျှခြင်းစနစ်အား ပေါင်းစပ်ပုံစံဖြင့် ဆန်းစစ်ကြည့်ကြပါစို့။

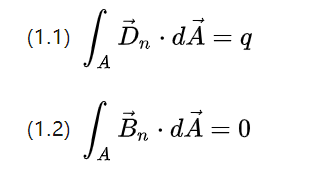
အထက်ဖော်ပြပါညီမျှခြင်းနှစ်ခုသည် ကွက်လပ်သိပ်သည်းဆ၏ စီးဆင်းမှုကို ဖော်ပြသည်၊ အသီးသီး၊ အထွက်အလားအလာပြောင်းလဲမှုရုပ်ပုံလွှာစုစုပေါင်းနှင့် အပိတ်အာကာသမျက်နှာပြင်ရှိ လှည့်ပတ်နေသော သံလိုက်စက်ကွင်း induction ပုံ စုစုပေါင်းကို ဖော်ပြသည်။

အထက်တန်းကျောင်းတွင် သင်ယူခဲ့သော အသိပညာအရ လျှပ်စစ်စက်ကွင်းအား ပွိုင့်အား လှုံ့ဆော်မှုဖြင့် ထုတ်ပေးနိုင်ပြီး သံလိုက်စက်ကွင်းအား သံလိုက်မိုနိုပိုလီမှ လှုံ့ဆော်ပေးနိုင်သော်လည်း လမ်းကြောင်းကို ချဲ့ထွင်ရန် ပိတ်ထားသောကြောင့် လျှပ်စစ်စက်ကွင်းသည် တက်ကြွနေပြီး သံလိုက်စက်ကွင်း၊ passive။

ထို့ကြောင့် စုစုပေါင်းအလားအလာ shift flux သည် စုစုပေါင်း charge q ဖြစ်ပြီး စုစုပေါင်း magnetic flux သည် 0 ဖြစ်သည်။

အထက်ဖော်ပြပါညီမျှခြင်းနှစ်ခုသည် စက်ကွင်းပြင်းထန်မှု၏ လှည့်ပတ်ပမာဏများ၊ စုစုပေါင်းလျှပ်စစ်စက်ကွင်းပြင်းထန်မှုနှင့် စုစုပေါင်းသံလိုက်စက်ကွင်းပြင်းထန်မှုကို ဖော်ပြသည်။

သံလိုက်အတက်အကျ၏ပြောင်းလဲမှုနှုန်းနှင့် အလားအလာပြောင်းလဲမှု (လက်ရှိပြင်းထန်မှု) တို့၏ ပြောင်းလဲမှုနှုန်းနှင့် သက်ဆိုင်သော၊ ပိတ်ထားသောနေရာမျဉ်းကွေးတစ်ခုပေါ်ရှိ မျဉ်းကွေး၏လမ်းကြောင်းတစ်လျှောက် တစ်ကွေ့အတွက်၊

Gauss နှင့် Stokes ဖော်မြူလာများသည် အထက်ဖော်ပြပါ ညီမျှခြင်းလေးခုကို ကွဲပြားမှုပုံစံအဖြစ် အောက်ပါအတိုင်း ပြန်လည်ရေးသားခွင့်ပြုပါသည်။

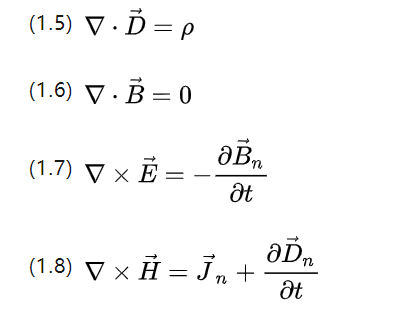
▽ လှည့်ပတ်တွက်ချက်ရန်၊ အားသွင်းကိုယ်ထည်သိပ်သည်းဆအတွက် P နှင့် လက်ရှိသိပ်သည်းဆအတွက် Jn ကိုတွက်ချက်ရန် ကွက်လပ်နှင့်လမ်းဆုံထုတ်ကုန်ကိုတွက်ချက်ရန် vector dot ထုတ်ကုန်ဖြင့် Nabla အော်ပရေတာအတွက် ▽။

အထက်ဖော်ပြပါ ညီမျှခြင်းများသည် ac induction motor စနစ်များအားလုံးတွင် ဖြစ်ပေါ်သည့် လျှပ်စစ်သံလိုက်အပြုအမူအားလုံးကို အခြေခံအားဖြင့် ဖော်ပြနိုင်သည်။

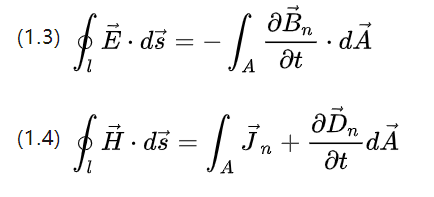
1.2 လျှပ်စစ်စွမ်းအင်အတွက် အရာဝတ္ထု polarization နှင့် magnetization

အသုံးချလျှပ်စစ်လည်ပတ်သံလိုက်စက်ကွင်းတစ်ခုတွင်၊ အရာဝတ္တုမော်လီကျူးများသည် လယ်ကွင်း၏ခိုင်ခံ့မှုအပေါ် သက်ရောက်မှုရှိသောကြောင့် polarity သည် ၎င်းတို့၏ ဦးတည်ရာကို ပြောင်းလဲသွားမည်ဖြစ်သည်။

မူလသံလိုက်စက်ကွင်းကြောင့် အရွယ်အစားအမျိုးမျိုးရှိသော မညီညာစွာစီစဉ်ထားသော မော်လီကျူးအုပ်စုများဖြင့် ဖွဲ့စည်းထားသော လျှပ်စစ်ဒိုမိန်းများသည် ပိုလာကွဲသွားမည်ဖြစ်ပြီး တာဝန်ခံဖြန့်ဖြူးမှု တိမ်းညွှတ်မှု ပေါင်းစည်းသွားမည်ဖြစ်သည်။

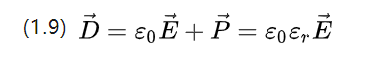
E0=8.854187817*10-12F/m သည် လေဟာနယ်၏ခွင့်ပြုချက်ဖြစ်ပြီး၊ ၎င်းသည် လေဟာနယ်ဒိုင်အီလက်ထရစ်ကိန်းသေလည်းဖြစ်ပြီး P သည် ပစ္စည်း၏ဂုဏ်သတ္တိများဖြင့် ဆုံးဖြတ်သည့် နှိုင်းယှဥ်ကိန်းသေဖြစ်သည်။

(1.9) အသုံးချလျှပ်စစ်စက်ကွင်း၏ အလားအလာရှိသော ပြောင်းလဲမှုသိပ်သည်းဆနှင့် သက်ဆိုင်သော polarization ပြင်းထန်မှု ရုပ်ပုံတို့ကို အတူတကွ ဖော်ပြသည်။

အသုံးချသံလိုက်စက်ကွင်းတစ်ခုတွင်၊ သက်ဆိုင်ရာသံလိုက်ဒိုမိန်းများနှင့် သံလိုက်ဓာတ်အား အစွမ်းသတ္တိများကို တူညီသောနည်းဖြင့် ရရှိနိုင်သည်။

လျှပ်စစ်စက်ကွင်းနှင့်မတူဘဲ၊ ပစ္စည်း၏သံလိုက်ဓာတ်အားသွင်းအားအားနှင့် လေဟာနယ်ပတ်ဝန်းကျင်၏ ခြားနားချက်ကိုဖော်ပြသည့် သံလိုက်ပိုလာရိုက်ချက်အား M ကို မိတ်ဆက်ပေးသည်။

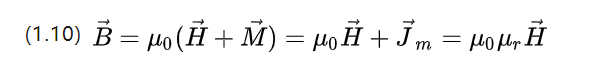
U0=4π*10-7 N.A-2 သည် လေဟာနယ် စိမ့်ဝင်နိုင်မှုဖြစ်ပြီး Ur သည် သံလိုက်စက်ကွင်းကို ဖြတ်သန်းခွင့်ပြုသည့် ပစ္စည်း၏ စွမ်းရည်ကို ဖော်ပြသည့် နှိုင်းရစိမ့်ဝင်နိုင်စွမ်းဖြစ်သည်။

အကယ်၍ ဥရ၊<=1 သည် သံလိုက်ဓာတ်ဖြစ်ပြီး၊ ပစ္စည်းသည် သံလိုက်စက်ကွင်း၏ ဖြတ်သန်းမှုကို တားဆီးသည်။ ပုံသည် paramagnetic ဖြစ်ပါက၊ ပစ္စည်းသည် သံလိုက်စက်ကွင်း၏ ဖြတ်သန်းမှုကို လိုက်နာသည်။

အကယ်၍ ဥရ၊>=1o 5 သည် ferromagnetic ဖြစ်ပြီး၊ ferro-cobalt nickel ကဲ့သို့သော ပစ္စည်းသည် သံလိုက်ဓာတ်ပြုပြီးနောက် သံလိုက်စက်ကွင်းကို မြှင့်တင်ပေးပါသည်။ ထို့နောက် remanent magnetism ဟုခေါ်သော သံလိုက်စက်ကွင်းကို ဖယ်ရှားပြီးနောက် သံလိုက်စက်ကွင်း၏ ခိုင်ခံ့မှုကို ထိန်းသိမ်းပါ။

မော်တာလည်ပတ်မှုဖြစ်စဉ်တွင် စဉ်ဆက်မပြတ် သံလိုက်ပြုလုပ်ခြင်း နှင့် demagnetization များရှိနေမည်ဖြစ်သဖြင့် မတူညီသော ပစ္စည်းများ၏ hysteresis လိုင်းများကို စစ်ဆေးခြင်းကိုလည်း ဂရုပြုသင့်ပါသည်။

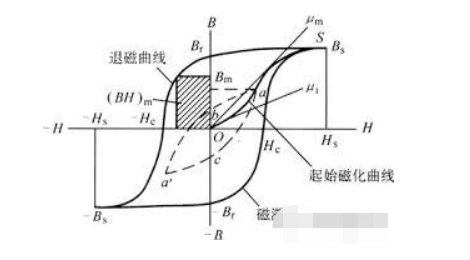
Hysteresis မျဉ်းသည် အသုံးချသံလိုက်စက်ကွင်းအား H ၏ လုပ်ဆောင်ချက်အောက်တွင် နယ်ပယ်အား ခွန်အားတိုးလာသည်နှင့်အမျှ သံလိုက်ပစ္စည်းတစ်ခု၏ သံလိုက်ဓာတ်တိုးလာမှုကို ဖော်ပြသည်။

ဤသံလိုက် induction သည် သံလိုက်ဓာတ် ပြည့်ဝမှုသို့ ရောက်ရှိပြီးနောက် နယ်ပယ်၏ ခွန်အားကို မလိုက်နာပါ။

သံလိုက်ဓာတ်ပြည့်ဝမှုသို့ရောက်ရှိပြီးနောက်၊ နယ်ပယ်ခွန်အားတိုးလာမှုကို လိုက်နာရန်ခက်ခဲသည်။ ပြင်ပသံလိုက်စက်ကွင်း ခွန်အားသည် သုညသို့ ဖြည်းညှင်းစွာ လျော့ကျသွားသောအခါ၊ သုညမှတ်ကို ကျော်သွားသောအခါတွင် demagnetization မျဉ်းကွေးသည် မမြဲသော သံလိုက်လှိုင်း B ကို ဆက်လက်ထိန်းသိမ်းထားဆဲဖြစ်သည်ကို တွေ့မြင်နိုင်သည်။

ဤတည်မြဲသော သံလိုက်ဓာတ်သည် အမြဲတမ်းသံလိုက်များ ထုတ်လုပ်ခြင်း၏ ယေဘူယျနိယာမဖြစ်သည်၊ ဆိုလိုသည်မှာ၊ လမ်းကြောင်းမှန်အတိုင်း ဖြည်းဖြည်းချင်း demagnetization ဖြင့် နောက်တွင် လမ်းကြောင်းမှန်သံလိုက်ခြင်းကို ပြသသည်။ ပြောင်းပြန်သံလိုက်စက်ကွင်းကို အသုံးချသောအခါ သံလိုက်လျှပ်ကူးအားသည် သုညသို့သွားသည် သို့မဟုတ် ဆန့်ကျင်ဘက်ဦးတည်ချက်တွင်ပင် တိုးလာပြီး ဤပိုလျှံမှုကို coercivity H ဟုခေါ်သည်။

1.3 လျှပ်စစ်သံလိုက်စွမ်းအားနှင့် စက်မှုစွမ်းအင်

မော်တာ၏ အကြီးမားဆုံးတန်ဖိုးမှာ လျှပ်စစ်စွမ်းအင်မှ စက်စွမ်းအင်သို့ ပြောင်းလဲခြင်းကို သိရှိနားလည်ရန်၊ ပြင်ပတွင် အလုပ်လုပ်ရန်နှင့် ပစ်မှတ်ကို အကောင်အထည်ဖော်ရန် ဖြစ်သည်။

သံလိုက်စက်ကွင်းရှိ အားသွင်းထားသော အမှုန်အမွှားများ၏ ရွေ့လျားမှုသည် ရွေ့လျားမှု၏ ဦးတည်ရာဆီသို့ Lorentz force ကို သက်ရောက်သည်၊ ဦးတည်ချက်၊

I သည် လျှပ်စီးကြောင်းကို ဦးတည်သည့် သံလိုက်စက်ကွင်းရှိ conductor ၏ ထိရောက်သော အရှည်ဖြစ်သည်။

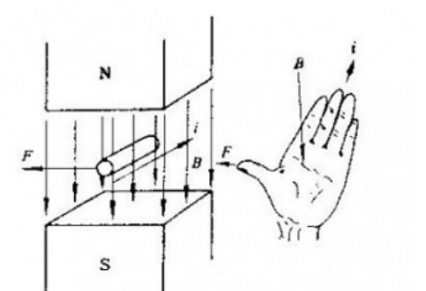
Electrostatic Field Fe=qE တွင် သက်ဆိုင်သော လျှပ်စစ်စက်ကွင်း တွန်းအားလည်း ရှိပါသည်။

သံလိုက်နှင့်လျှပ်စစ်စက်ကွင်းနှစ်ခုစလုံးသည် ၎င်းတို့ဘာသာနယ်ပယ်များဖြစ်ကြပြီး ၎င်းတို့တွင်ရှိသော အားသွင်းမှု သို့မဟုတ် လက်ရှိဒြပ်စင်သို့ သက်ရောက်သည့်အင်အားသည် ထုထည်နှင့် အကွက်သိပ်သည်းဆပေါ်တွင်မူတည်သောကြောင့် သက်ဆိုင်ရာနယ်ပယ်အား နယ်ပယ်၏စည်းကမ်းချက်များအရ ဆန်းစစ်နိုင်ပါသည်။

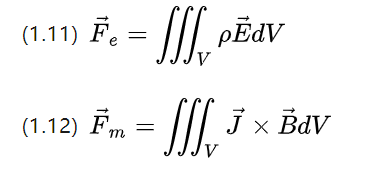
အထက်ပါညီမျှခြင်းနှစ်ခုသည် symmetry ကိုဆက်လက်ထိန်းသိမ်းထားဆဲဖြစ်ပြီး၊ လျှပ်စစ်စက်ကွင်းလယ်ကွင်းအားကြောင့် အချို့သောထုထည်တစ်ခုတွင် အားသွင်းသိပ်သည်းဆသည် electric force density fe = pE ကိုထုတ်လုပ်ပေးပါသည်။

သံလိုက်စက်ကွင်း ခွန်အားကြောင့် အချို့သော ထုထည်တစ်ခုတွင် လက်ရှိသိပ်သည်းဆ J သည် သံလိုက်စွမ်းအားသိပ်သည်းဆ Fm = J*B (အထက် ညီမျှခြင်း (1.12) ကို isotropic ပစ္စည်းများနှင့် အဆက်မပြတ် လျှပ်စီးကြောင်းအတွက် အသုံးပြုရမည်)။

ဤအသုံးအနှုန်းသည် လျှပ်စစ်သံလိုက်စက်ကွင်း၏ စွမ်းအင်နှင့် စွမ်းအင်သိပ်သည်းဆကို တိုက်ရိုက်စစ်ဆေးရန် ကျွန်ုပ်တို့အား လှုံ့ဆော်ပေးပါသည်။

ဤနည်းအားဖြင့်၊ သက်ဆိုင်ရာလျှပ်စစ်သံလိုက်စွမ်းအားသိပ်သည်းဆကိုရရှိရန် gradient ကိုရှာဖွေခြင်းဖြင့် အချို့သောနေရာများတွင် လျှပ်စစ်သံလိုက်ဖြစ်နိုင်ချေစွမ်းအင်ကို ဆုံးဖြတ်နိုင်ပြီး၊ ထို့ကြောင့် စုံစမ်းဆဲအရာဝတ္ထုပေါ်ရှိ စုစုပေါင်းလျှပ်စစ်သံလိုက်စွမ်းအားကို ရှာဖွေနိုင်သည်။

1.4 Coil မော်ဒယ်

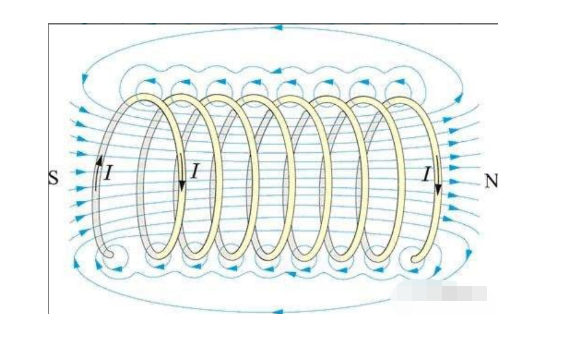
ကွိုင်သည် လျှပ်ကူးပစ္စည်း မော်တာများ ၏ စံနမူနာကို ပုံဖော်ကာ အခြေခံ ဒြပ်စင် တစ်ခု ဖြစ်ပြီး ac မော်တာ ၏ ဆားကစ် မော်ဒယ် နှင့် အရာဝတ္တု ၏ ရုပ်ပိုင်းဆိုင်ရာ မော်ဒယ် ကို ပေါင်းကူး ပေးသည် ။

အားဖြည့်စပယ်ယာ၏ ဖြောင့်တန်းသောအပိုင်းသည် ၎င်းပတ်ပတ်လည်ရှိ toroidal သံလိုက်စက်ကွင်းကို ထုတ်ပေးသည် (ညီမျှခြင်း 1.4 အရ)။

အစနှင့်အဆုံးတွင် conductor ကိုပိတ်သောအခါ၊ toroidal field သည် solenoid ကဲ့သို့သော conductor ring မှတဆင့်ဒေါင်လိုက်ဖြတ်သွားသော conductor ring ၏အလယ်ဗဟိုတွင် toroidal field သည် သံလိုက်လိုင်းများဖြစ်လာသည်။

စွမ်းအင်ရှိသော စပယ်ယာပေါ်ရှိ လက်ရှိကိုသာ ထည့်သွင်းစဉ်းစားခြင်းဖြင့်၊ (1.4) သည် အောက်ပါတို့ကို ရိုးရှင်းစေသည်။

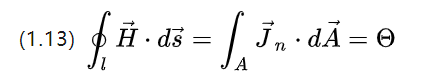
သံလိုက်စွမ်းအား ( magnetische Durchfluchtung ) သည် excitation field ၏ ခွန်အားအရင်းအမြစ်ဖြစ်သည့် [A] ရှိ အပိတ်စပယ်ယာ၏ အပိုင်းကို ဖြတ်သွားသော စုစုပေါင်းလက်ရှိ၏ အင်အားဖြစ်သည်။

လက်တွေ့တွင် စွမ်းအင်ရှိသော ဝါယာကြိုးသည် ကွိုင်တစ်ခုသို့ ဒဏ်ရာရသွားမည်ဖြစ်ပြီး၊ ဝါယာလျှပ်စီးကြောင်းကို ခွဲခြားသတ်မှတ်ထားပြီး (1.13) အဖြစ် ပြန်လည်ရေးသားထားသည်။

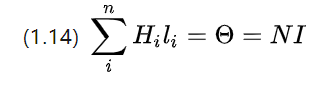
N သည် ကွိုင်ရှိ အကွေ့အကောက် စုစုပေါင်း အရေအတွက်၊ ဆိုလိုသည်မှာ အလှည့်အပြောင်း အရေအတွက်။

အလှည့်အပြောင်း အရေအတွက် ပိုများလျှင် စုစုပေါင်း လျှပ်စီးကြောင်း ပိုများသည်၊ သံလိုက် အလားအလာ ပိုများလာပြီး သံလိုက်စက်ကွင်း အားကောင်းလေ စိတ်လှုပ်ရှားနိုင်သည်ကို တွေ့မြင်နိုင်သည်။

(1.3) ဖြင့်ဖော်ပြထားသော ဖြစ်စဉ်တစ်ခုဖြစ်သည့် ဝါယာ၏အစွန်းနှစ်ဖက်ရှိ အချိန်ကွဲပြားသော သံလိုက်စက်ကွင်းရှိ တစ်ချက်လှည့်ကွိုင်တစ်ခုသည် ဗို့အားကို လှုံ့ဆော်ပေးမည်ဖြစ်သည်။

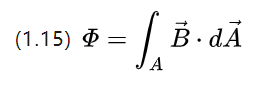
(1.3) အစားထိုးခြင်းဖြင့် ရရှိနိုင်သော သံလိုက်လှိုင်းသိပ်သည်းဆကို သံလိုက်ဓာတ်အားသွင်းခြင်းအဖြစ်လည်း အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်ကို နားလည်နိုင်ပါသည်။

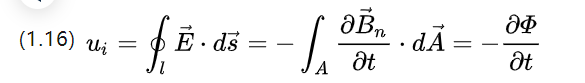
Ui သည် induced electric potential ဖြစ်ပြီး flux ပြောင်းလဲမှုပုံစံနှစ်မျိုးကိုစဉ်းစားပါ၊ တစ်ခုသည် coil ဧရိယာကိုပြောင်းလဲရန်ဖြစ်သော်လည်း flux density ကိုပြောင်းလဲပြီးနောက်အောက်ပါအတိုင်းဖြစ်သည်။

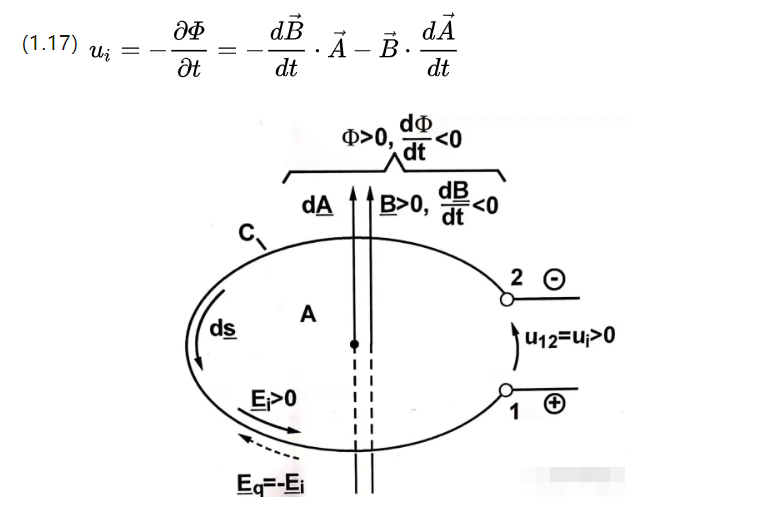
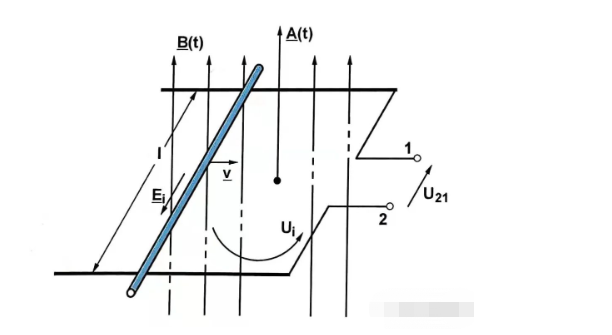
ယခင်အပိုင်းသည် တရားဝင်ပြောင်းလဲထားသော induction အလားအလာဖြစ်ပြီး နောက်အပိုင်းမှာ ဘာသာပြန်ထားသော induction ဖြစ်နိုင်ချေဖြစ်သည်။

ယခင်သည် အချိန်-ကွဲပြားသော သံလိုက် flux သိပ်သည်းဆ ရှိပြီး နောက်ပိုင်းတွင် အချိန်-ကွဲပြားသည့် ထိရောက်သော ကွိုင်ဧရိယာ ရှိသည်။

ဤနိယာမကို အထက်တန်းကျောင်းရူပဗေဒတွင် ဖော်ပြထားပြီး ပုလွေသီအိုရီဟုလည်း ခေါ်သည်။

ကွိုင်တစ်ခုတွင် အလှည့်များစွာရှိသောအခါ၊ စုစုပေါင်းထိရောက်သော flux သည် ချဲ့ထားသောကွိုင်အလှည့်များ၏ ကိန်းပြည့်တစ်ခုဖြစ်ပြီး၊ ထို့ကြောင့် သံလိုက်ကွင်းဆက်၏သဘောတရားကို မိတ်ဆက်ပေးသည်။

ကွင်းဆက်ကို အောက်ပါပုံတွင် သတ်မှတ်ထားပါသည်။

သံလိုက်ကွင်းဆက်သည် သံလိုက်လှိုင်းများကဲ့သို့ စကေးပမာဏတစ်ခုဖြစ်ကြောင်း သတိပြုပါ။ လက်ရှိပြောင်းလဲမှုတစ်ခုသည် flux အပြောင်းအလဲကိုဖြစ်ပေါ်စေနိုင်သောကြောင့်၊ သဘောထားသည် flux ပြောင်းလဲမှုကိုတားဆီးရန်ဖြစ်သည်၊၊

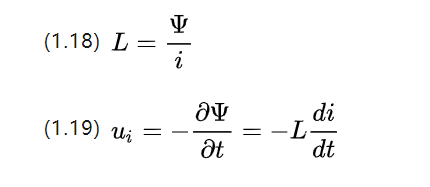
i သည် မတူညီသော လက်ရှိပြင်းထန်မှုဖြစ်ပြီး L သည် Henry [H] တွင် self-inductance coefficient ဖြစ်ပြီး ၎င်း၏အရွယ်အစားသည် ကွိုင်ထုထည်ပုံသဏ္ဍာန်၊ အလှည့်အပြောင်းအရေအတွက်နှင့် သံလိုက်စိမ့်ဝင်နိုင်စွမ်းတို့နှင့် ဆက်စပ်နေသည်။

သံလိုက်စိမ့်ဝင်နိုင်စွမ်းကို တိုးမြင့်စေရန်အတွက် induction motors များတွင် coil များကို သံ core ကဲ့သို့သော coil ၏အလယ်တွင် ferromagnetic material ဖြင့်ပြုလုပ်ထားသောကြောင့် coil သည် iron core တွင်အနာဖြစ်စေသောကြောင့် winding ဟုခေါ်သည်။

မျဉ်းကြောင်းတူသော တစ်သားတည်းဖြစ်တည်နေသော ပစ္စည်း၏ အပိုင်းအတွက်၊ ၎င်း၏ အလိုအလျောက် လျှပ်ကူးနိုင်စွမ်း ကိန်းဂဏာန်းအား အောက်ပါညီမျှခြင်းဖြင့် ခန့်မှန်းနိုင်သည်

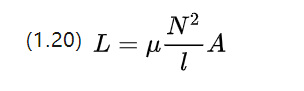
Self-inductance သည် dc လျှပ်စစ်မော်တာ၏ လျှပ်စီးကြောင်းပြောင်းလဲမှုများကို ဟန့်တားရန် တွန်းအားပေးသည့် လျှပ်စီးဗို့အားကို တွန်းလှန်ရန် ၎င်း၏ကိုယ်ပိုင် လက်ရှိပြောင်းလဲမှုများ၏ ကွိုင်တစ်ခုဖြစ်သည်။

ကွိုင်နှစ်ခုသည် တစ်ခုနှင့်တစ်ခု နီးကပ်လာသောအခါတွင် ၎င်းတို့၏ ကိုယ်ပိုင် inductance အပြင် အနီးနားရှိ ကွိုင်များကြောင့်လည်း လက်ရှိပြောင်းလဲမှုများနှင့် အပြန်အလှန် inductance၊

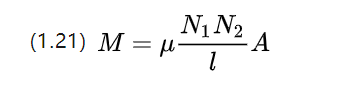
linear identities ပါရှိသော ပစ္စည်းများ၏ အပြန်အလှန် inductance ၏ coefficient သည် အထက်ပါညီမျှခြင်းဖြင့် အနီးစပ်ဆုံးဖြစ်ပြီး အပြန်အလှန် inductance သည် တစ်ချိန်တည်းတွင် coil နှစ်ခု၏ အလှည့်အရေအတွက်ကြောင့် သက်ရောက်မှုရှိကြောင်း ပြသသည်။

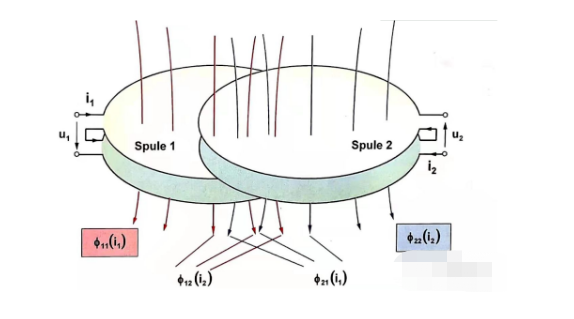
ကပ်လျက်ကွိုင်နှစ်ခု၏ ခံနိုင်ရည်အားကို လျစ်လျူရှုပြီး မိမိဘာသာနှင့် အပြန်အလှန် inductance ကို စစ်ဆေးခြင်းဖြင့် ဗို့အားညီမျှခြင်းကို ပုံ 1.5 မှ dc မော်တာများအကြောင်း ဖော်ပြနိုင်ပါသည်။

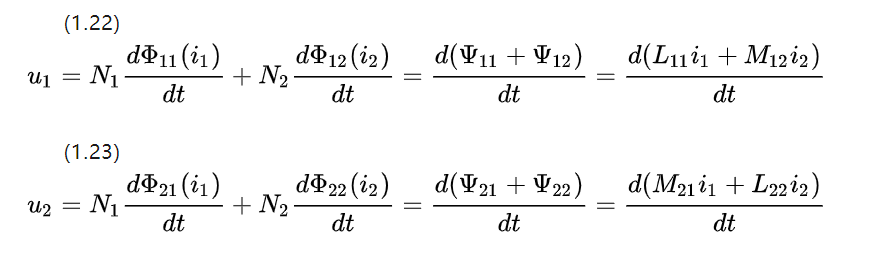
အချိတ်အဆက် အစိတ်အပိုင်းများသည် တူညီသော ပစ္စည်း ကန့်သတ်ချက်များ နှင့် ပုံသဏ္ဍာန် ရှိသည် ဖြစ်သောကြောင့် ရရှိလာသော အပြန်အလှန် လျှပ်ကူးပစ္စည်း ကိန်းများသည် M12=M21 နှင့် တူညီပါသည်။

ထို့ကြောင့် ကွိုင်တစ်ခုစီရှိ coupling chains အရွယ်အစားသည် သက်ဆိုင်ရာ rotor windings coil ပေါ်ရှိ လက်ရှိ ခွန်အားနှင့် အချိုးကျပါသည်။ ။

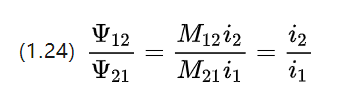
လျှပ်စစ်စွမ်းအင်နှင့် သံလိုက်ပတ်လမ်းများအတွက် 1.5 Ohm သီအိုရီ

အလယ်တန်းကျောင်းတွင် ကျွန်ုပ်တို့သည် လျှပ်ကူးပစ္စည်း၏ ခံနိုင်ရည်သည် ဗို့အားနှင့် လျှပ်စီးကြောင်း၏ အချိုးအဆဖြစ်ပြီး အစွန်းနှစ်ဖက်ရှိ ခံနိုင်ရည်ရှိပစ္စည်းကို ဖော်ပြရန်အတွက် ဖော်မြူလာတစ်ခုရှိကြောင်း Ohm ၏ သီအိုရီကို လေ့လာခဲ့သည်။

Q သည် conductivity ဖြစ်သည့် Resciprocal P ၏ အတိအကျဖြစ်ပြီး လျှပ်စီးကြောင်းလုပ်ဆောင်နိုင်စွမ်းကို ဖော်ပြသည်။

ခံနိုင်ရည်အား အသုံးချခြင်းအပြင်၊ လျှပ်စစ်မော်တာ အလုပ်လုပ်သောအခါတွင် လျှပ်ကူးပစ္စည်းပုံဖြင့် ဗို့အားနှင့် လျှပ်စီးကြောင်းကြား ဆက်နွယ်မှုကိုလည်း ဖော်ပြနိုင်သည်။

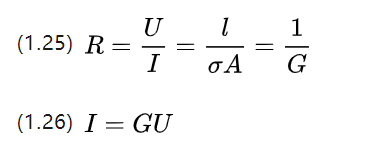
ယခု ယူနစ်ဧရိယာအလိုက် လက်ရှိပြင်းအားကို စစ်ဆေးပါ၊ ဆိုလိုသည်မှာ၊ လက်ရှိသိပ်သည်းဆ J = I/A e (e သည် ယူနစ် vector) ဖြင့် လက်ရှိသိပ်သည်းဆကို ac မော်တာများအတွက် လျှပ်စီးကြောင်းကို ညွှန်ပြသည့် vector တစ်ခုအနေဖြင့် စစ်ဆေးပါ။

၎င်းကို ဗို့အားညီမျှခြင်း U=E.l နှင့် (1.25) ကို (1.26) အဖြစ် ပြန်လည်ရေးသားနိုင်သည်။

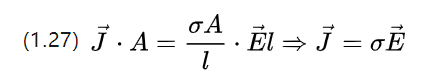
အထက်ဖော်ပြပါညီမျှခြင်းသည် အဏုစကုပ်အဆင့်တွင် Ohm ၏သီအိုရီကို ဖော်ပြသည်၊ ဆိုလိုသည်မှာ၊ conductor နှင့် ဆက်နွှယ်နေသော ကွင်းပြင်ခိုင်ခံ့မှုဆိုင်ရာ လက်ရှိသိပ်သည်းဆ၏ကွဲလွဲမှုကို ဖော်ပြသည်။

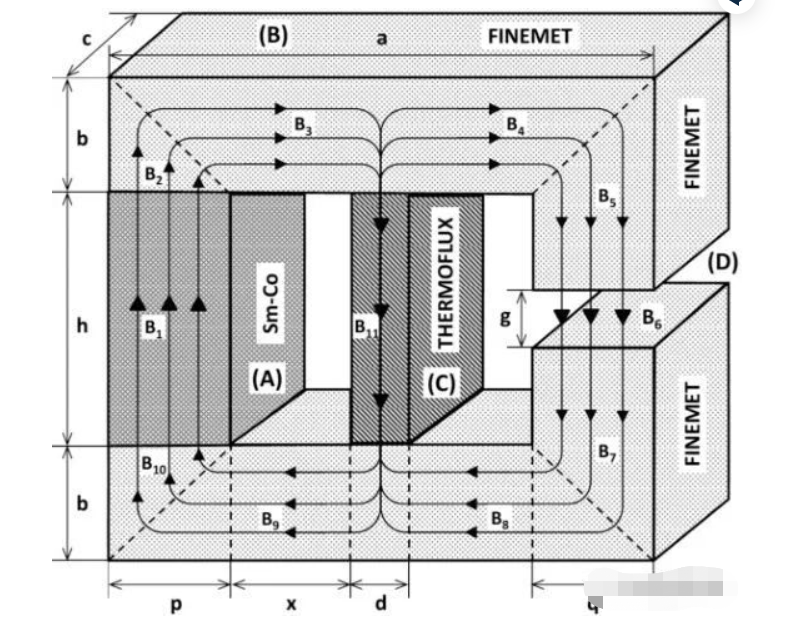
Lm သည် သံလိုက်ပတ်လမ်း၏ အပိုင်းတစ်ခုမှတဆင့် သံလိုက်အတက်အကျ၏ ထိရောက်သောအရှည်ဖြစ်ပြီး A သည် သက်ဆိုင်ရာ flux ဧရိယာဖြစ်သည်။

အထက်ပါညီမျှခြင်းသည် ခုခံမှုဖော်မြူလာနှင့် အလွန်ဆင်တူသည်။

ကျွန်ုပ်တို့သည် magnetoresistance ဖော်မြူလာကို နောက်တစ်ကြိမ် ပုံပျက်စေကာ ဆက်လက်၍ ရယူနိုင်ပါသည်။

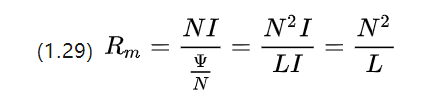
ယူနစ်များတွင် magnetoresistance သည် အမှန်တကယ် inductance coefficient ၏ ပြောင်းပြန်ဖြစ်သည်ကို တွေ့နိုင်ပါသည်။

လျှပ်ကူးပုံသဘောတရားနှင့် ယှဉ်တွဲကာ သံလိုက်လျှပ်ကူးပုံ A ( magnetische Leitwert ၊ [H] သို့မဟုတ် [Ωs]) ကို ရရှိသည်။

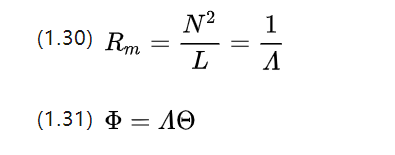
ဆားကစ်တွင် ကျွန်ုပ်တို့သည် (1.26) အတွက် ကွဲပြားသောဒြပ်စင်များကို ရှာတွေ့ပြီး အဏုကြည့်မြင်နိုင်သော Ohm ၏ သီအိုရီကို ရရှိသည်၊ ထို့ကြောင့် အဏုကြည့်နိုင်သော Ohm ၏ သီအိုရီသည် အဘယ်နည်း။

သံလိုက် flux သည် flux density B ပါရှိကြောင်း သတိပြုမိပြီး ညီမျှခြင်း (1.31) ကို ပြန်ရေးနိုင်သည် ။

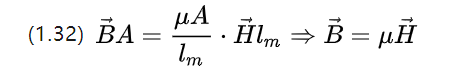
ထို့ကြောင့် အဏုကြည့်သံလိုက်ပတ်လမ်း Ohm ၏ သီအိုရီသည် ညီမျှခြင်း (1.10) ဖြစ်ပြီး အောက်ရှိ သံလိုက်စက်ကွင်း ခွန်အားသည် အဆက်မပြတ် သံလိုက်စက်ကွင်း၏ သံလိုက်စက်ကွင်းမှ ရရှိသော flux density ဖြစ်သည်။

တွန့်ဆုတ်မှု၏ တွက်ချက်မှုဆိုင်ရာ ခွဲခြမ်းစိတ်ဖြာမှုကို မော်တာအကွေ့အကောက်များတိုင်၊ အူတိုင်တစ်ခုလုံးရှိ flux ၏ သေးငယ်သောဒြပ်စင်ခွဲခြမ်းစိတ်ဖြာမှုကို သိရှိရန် အသုံးပြုနိုင်ပြီး၊ သီးခြားကန့်သတ်ဒြပ်စင်ခွဲခြမ်းစိတ်ဖြာမှု FEM (Finite-Elemente-Methode) ကို သိရှိနိုင်မည်ဖြစ်သည်။ သံလိုက်ပတ်လမ်းတစ်ခုလုံး၏။

အလွန်နားလည်လွယ်ပြီး အဆင်ပြေသော သံလိုက်ပတ်လမ်းရှိ ဆားကစ်အတွက် Kirchhoff ၏ သီအိုရီကို အသုံးချနိုင်သည်။

မှတ်ချက်ဧရိယာရှိ လျှပ်စစ်မော်တာများအကြောင်း နောက်ထပ်အချက်အလက်များကို ကျွန်ုပ်တို့နှင့်မျှဝေရန် ကြိုဆိုပါသည်။

လျှပ်စစ်မော်တာနှင့်ပတ်သက်သည့် မည်သည့်စုံစမ်းမေးမြန်းမှုများကိုမဆို ကျေးဇူးပြု၍ ပရော်ဖက်ရှင်နယ်လျှပ်စစ်မော်တာသို့ ဆက်သွယ်ပါ။ ထုတ်လုပ်သူ ၌ တရုတ် ဖော်ပြပါအတိုင်း: