1. المبدأ الفيزيائي لعمل المحرك الكهربائي
1.1 نظام معادلات ماكسويل
المحرك الكهربائي هو محول طاقة يحول باستمرار الطاقة الكهرومغناطيسية والطاقة الميكانيكية.
عندما يتم إدخال الطاقة الكهربائية ، يمكن للمحرك الكهربائي إخراج عزم الدوران والطاقة الميكانيكية باستمرار.
أي المحرك الكهربائي على العكس من ذلك ، إذا دفعت قوة خارجية عمود المحرك الكهربائي بشكل مستمر وأدخلت الطاقة الميكانيكية ، يمكن للمحرك الكهربائي إخراج الجهد والطاقة الكهربائية باستمرار من طرف السلك في الاتجاه المعاكس ، أي المولد.
تاريخيًا ، كان المحول الساكن يُحسب أيضًا كمحرك كهربائي ، لكنه تطور تدريجيًا ليشير حصريًا إلى المحركات والمولدات الكهربائية.
من مزايا المحركات الكهربائية أن خسائرها صغيرة نسبيًا ، لذا فهي تحقق كفاءة عالية.
يمكن أن تحقق المحركات الكهربائية الكبيرة كفاءات تصل إلى 99٪.

عند الحديث عن الأنظمة الكهرومغناطيسية، فإن نظام معادلات ماكسويل أمر لا مفر منه.
في العالم المجهري وحتى في العالم المجهري ،
يمكن استخدام نظام معادلات ماكسويل بفعالية كبيرة لوصف خصائص النظام.
تم تلخيص نظام معادلات ماكسويل من الدراسات السابقة للظواهر الكهرومغناطيسية.
هناك أربع معادلات أساسية للغاية ، سواء في شكل تفاضلي أو متكامل.
الآن دعونا نتفحص نظام معادلات ماكسويل في الصورة التكاملية.
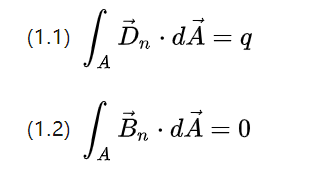
تصف المعادلتان المذكورتان أعلاه تدفق كثافة المجال ، على التوالي ، إجمالي صورة إزاحة احتمالية التدفق وإجمالي صورة تحريض المجال المغناطيسي الدوار في سطح فضاء مغلق
وفقًا للمعرفة المكتسبة في المدرسة الثانوية ، يمكن إنشاء المجال الكهربائي عن طريق إثارة الشحنة النقطية ، ولا يمكن إثارة المجال المغناطيسي بواسطة القطب الأحادي المغناطيسي ، ولكن لتمديد المسار مغلقًا ، وبالتالي فإن المجال الكهربائي نشط ، والمجال المغناطيسي هو سلبي.
لذا فإن إجمالي تدفق التحول المحتمل هو إجمالي الشحنة q ومجموع التدفق المغناطيسي هو 0.
تصف المعادلتان السابقتان كميات الدوران لشدة المجال ، وتكاملات شدة المجال الكهربائي الكلية وشدة المجال المغناطيسي الكلي.
يقابل معدل تغير التدفق المغناطيسي ومعدل تغير التحول المحتمل (شدة التيار) ، على التوالي ، لدورة واحدة على طول مسار المنحنى على منحنى الفضاء المغلق.
تسمح صيغتا Gauss و Stokes أيضًا بإعادة كتابة المعادلات الأربع المذكورة أعلاه في شكل تفاضلي على النحو التالي.
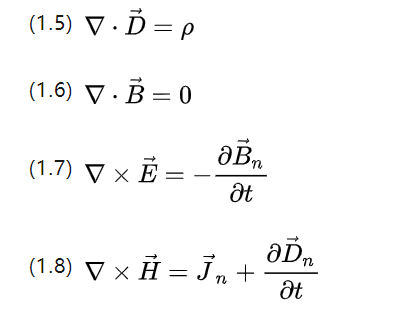
▽ لمشغل النبلة ، مع حاصل الضرب النقطي المتجه لحساب ناتج الانتثار والشوكة لحساب السبين ، و P لكثافة جسم الشحنة ، و J لكثافة التيار.
يمكن أن تصف المعادلات أعلاه بشكل أساسي كل السلوك الكهرومغناطيسي الذي يحدث في جميع أنظمة المحركات الحثية للتيار المتردد
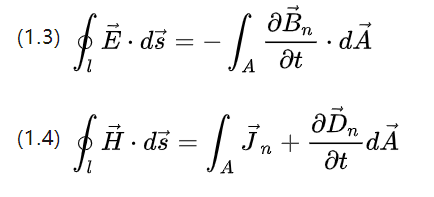
1.2 استقطاب ومغنطة المواد للطاقة الكهربائية
في مجال مغناطيسي دوار كهربائي مطبق ، ستغير جزيئات المادة اتجاهها لأن القطبية تتأثر بقوة المجال.
سيتم استقطاب المجالات الكهربائية التي تكونت بواسطة المجموعات الجزيئية الأصلية ذات الأحجام المختلفة المرتبة بشكل غير متساوٍ بسبب المجال المغناطيسي المطبق ، ويتقارب اتجاه توزيع الشحنة.
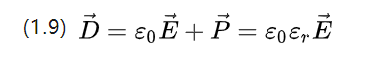
E0 = 8.854187817 * 10-12F / m هي سماحية الفراغ ، وهي أيضًا ثابت العزل الكهربائي للفراغ ، و P هو ثابت العزل النسبي ، والذي تحدده خصائص المادة نفسها.
يصف (1.9) كثافة التحول المحتمل للمجال الكهربائي المطبق وصورة شدة الاستقطاب المقابلة معًا.
في المجال المغناطيسي المطبق ، يمكن الحصول على المجالات المغناطيسية المقابلة وقوة المغنطة بنفس الطريقة.
على عكس المجال الكهربائي ، يتم إدخال قوة استقطاب مغناطيسي M ، والتي تصف الفرق بين قوة الحث المغناطيسي للمادة وتلك الخاصة ببيئة الفراغ.
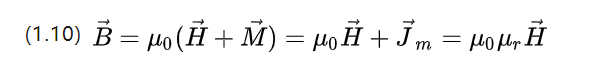
U0 = 4π * 10-7 NA-2 هي نفاذية الفراغ و Ur هي النفاذية النسبية ، والتي تصف قدرة المادة على السماح لمجال مغناطيسي بالمرور.
إذا أور<= 1 مضاد للمغناطيسية ، المادة تمنع مرور مجال مغناطيسي ؛ إذا كانت الصورة مغناطيسية ، فإن المادة تتوافق مع مرور مجال مغناطيسي.
إذا أور>= 1o 5 مغنطيسية حديدية ، المواد مثل النيكل الكوبالت الحديدي ستعزز المجال المغناطيسي بعد المغنطة. ثم تحتفظ بقوة معينة من المجال المغناطيسي بعد إزالة المجال المغناطيسي ، وهو ما يسمى بالمغناطيسية المتبقية.
في عملية تشغيل المحرك ، سيكون هناك مغنطة وإزالة مغناطيسية ثابتة ، لذلك يجب الانتباه أيضًا إلى فحص خطوط التباطؤ للمواد المختلفة.
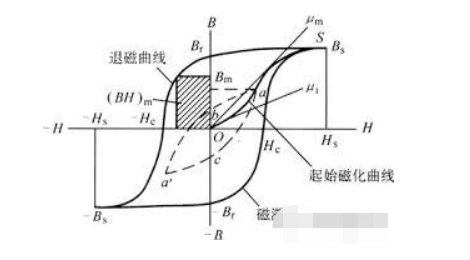
يصف خط التخلفية الحث المغناطيسي المتزايد لمادة مغناطيسية حيث تزداد شدة المجال تحت تأثير المجال المغناطيسي المطبق للقوة H.
لا يتبع هذا الحث المغناطيسي شدة المجال بعد الوصول إلى التشبع المغناطيسي.
بعد الوصول إلى التشبع المغناطيسي ، من الصعب متابعة الزيادة في شدة المجال. عندما تنخفض شدة المجال المغناطيسي الخارجي ببطء إلى الصفر ، يمكن ملاحظة أن منحنى إزالة المغناطيسية لا يزال يحتفظ بالمغناطيسية المتبقية B عندما يتجاوز نقطة الصفر.
تُظهر هذه المغنطة المتبقية المبدأ العام لتصنيع المغناطيس الدائم ، أي المغنطة الاتجاهية متبوعة بإزالة المغناطيسية التدريجية. عندما يتم تطبيق المجال المغناطيسي العكسي ، تذهب قوة الحث المغناطيسي إلى الصفر أو حتى تزداد في الاتجاه المعاكس ، ويسمى هذا الفائض بالإكراه H.
1.3 القوة الكهرومغناطيسية والطاقة الميكانيكية
أعظم قيمة للمحرك هي تحقيق تحويل الطاقة الكهربائية إلى طاقة ميكانيكية ، والقيام بعمل خارجي وتنفيذ الحركة المستهدفة.
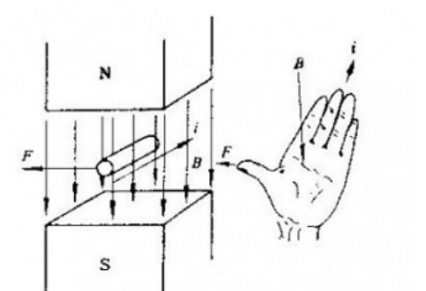
تخضع حركة الجسيم المشحون في مجال مغناطيسي لقوة لورنتز المتعامدة مع اتجاه الحركة ، والتي يكون تعبيرها المجهري هو قوة الأمبير Hm = Il * B ، والتي يمكن الحكم عليها باستخدام قاعدة اليد اليسرى لتحديد اتجاه،
I هو الطول الفعال للموصل في المجال المغناطيسي في اتجاه التيار.
هناك أيضًا قوة مجال كهربائي مقابلة في المجال الكهروستاتيكي Fe = qE.
والمجالان المغناطيسي والكهربائي هما مجالان بحد ذاته ، وتعتمد القوة المطبقة على الشحنة أو العنصر الحالي فيها على الحجم وكثافة المجال ، وبالتالي يمكن اختبار قوة المجال المقابلة من حيث المجال.
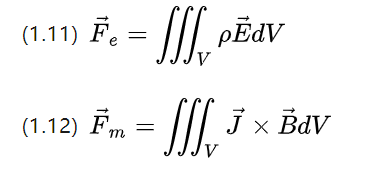
لا تزال المعادلتان السابقتان تحافظان على التناظر ، حيث تنتج كثافة الشحنة P في حجم معين بسبب مجال المجال الكهربائي كثافة القوة الكهربائية fe = pE ،
تنتج كثافة التيار J في حجم معين بسبب شدة المجال المغناطيسي كثافة القوة المغناطيسية Fm = J * B (يجب استخدام المعادلة أعلاه (1.12) في حالة المواد المتناحرة والتيار الثابت).
يلهمنا هذا التعبير لفحص الطاقة وكثافة الطاقة في المجال الكهرومغناطيسي بشكل مباشر.
بهذه الطريقة ، يمكن تحديد الطاقة الكامنة الكهرومغناطيسية عند نقطة معينة من خلال إيجاد التدرج للحصول على كثافة القوة الكهرومغناطيسية المقابلة وبالتالي إيجاد إجمالي القوة الكهرومغناطيسية على الجسم قيد التحقيق.
1.4 نموذج الملف
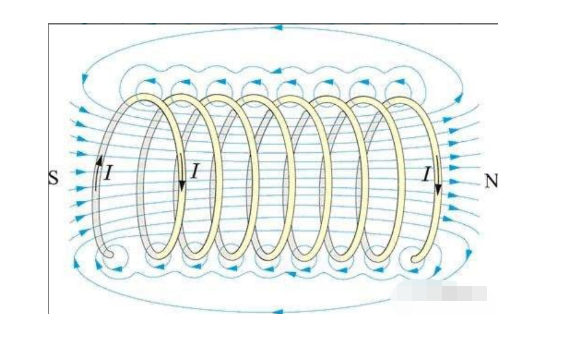
الملف هو عنصر أساسي يشكل نموذجًا للمحركات الحثية ، ويربط نموذج الدائرة لمحرك التيار المتردد والنموذج المادي للكائن.
يولد مقطع مستقيم من الموصل النشط مجالًا مغناطيسيًا حلقيًا حوله (وفقًا للمعادلة 1.4).
عندما يتم إغلاق الموصل في البداية والنهاية ، فإن المجال الحلقي يشكل خطوط قوة مغناطيسية في مركز الحلقة الموصلة التي تمر عموديًا عبر حلقة الموصل ، مثل الملف اللولبي.
بالنظر فقط إلى التيار الموجود على الموصل النشط ، (1.4) يبسط إلى:
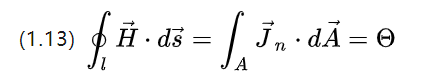
القوة الدافعة المغناطيسية (magnetische Durchfluchtung) ، والتي هي مصدر قوة مجال الإثارة ، هي أساسًا قوة التيار الكلي الذي يمر عبر قسم من الموصل المغلق في [A].
نظرًا لأنه من الناحية العملية سيتم لف السلك الذي تم تنشيطه في ملف ، فسيتم تحديد تيار السلك وإعادة كتابة (1.13) كـ
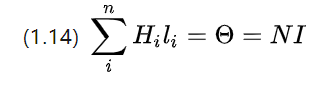
N هو العدد الإجمالي للملفات في الملف ، أي عدد الدورات.
يمكن ملاحظة أنه إذا كان عدد المنعطفات أعلى ، فإن التيار الإجمالي أعلى ، والجهد المغناطيسي أعلى ، ويمكن أن يكون المجال المغناطيسي أقوى.
الملف أحادي الدوران في مجال مغناطيسي متغير بمرور الوقت سوف يحفز جهدًا عند طرفي السلك ، وهي ظاهرة موصوفة في (1.3).
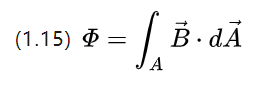
يمكن فهم أن الحث المغناطيسي يمكن أيضًا تفسيره على أنه كثافة التدفق المغناطيسي ، والتي يمكن الحصول عليها عن طريق الاستبدال (1.3)
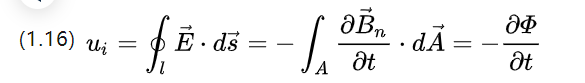
واجهة المستخدم هي الإمكانات الكهربائية المستحثة ، مع الأخذ في الاعتبار شكلين من أشكال تغيير التدفق ، أحدهما تغيير منطقة الملف ولكن تغيير كثافة التدفق ، ثم هناك ما يلي ؛
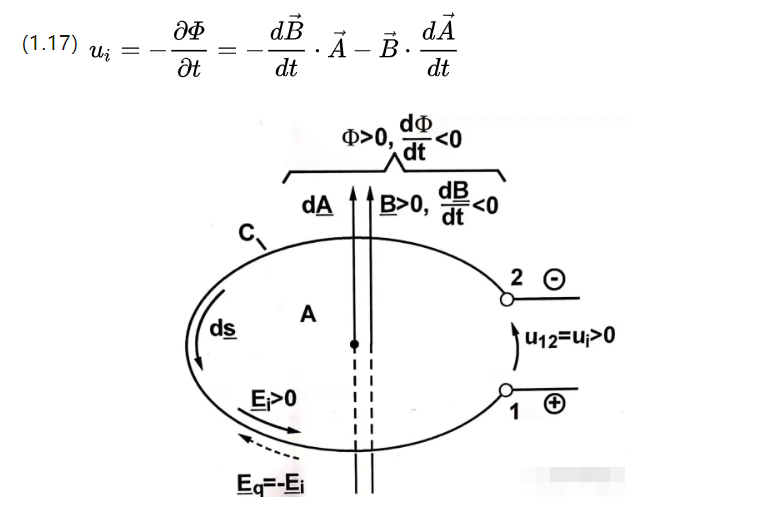
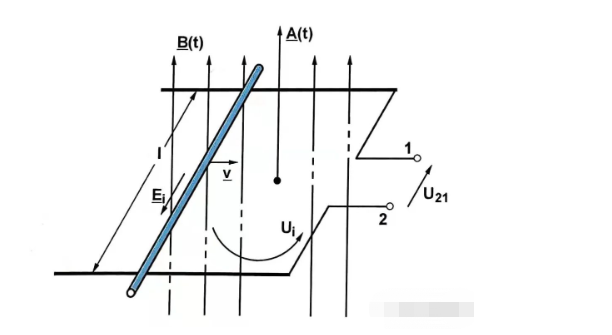
الجزء الأول هو إمكانات الحث التي تم تحويلها رسميًا والجزء الأخير هو إمكانات الحث المتحولة متعدية.
الأول له كثافة تدفق مغناطيسي متغيرة بمرور الوقت ، بينما يحتوي الأخير على منطقة ملف فعالة متغيرة بمرور الوقت.
تم ذكر مبدأ الحث هذا في فيزياء المدرسة الثانوية ويعرف أيضًا باسم نظرية الفلوت.
عندما يكون للملف العديد من المنعطفات ، فإن التدفق الفعال الإجمالي هو بالضبط عدد صحيح مضاعف لفائف الملف الموسع ، وبالتالي تقديم مفهوم السلسلة المغناطيسية.
يتم تعريف السلسلة في الشكل أدناه.
لاحظ أن السلسلة المغناطيسية عبارة عن كمية قياسية ، تمامًا مثل التدفق المغناطيسي. نظرًا لأن التغيير في التيار نفسه يمكن أن يتسبب أيضًا في حدوث تغيير في التدفق ، فإن الاتجاه هو إعاقة تغيير التدفق ، والذي يمكن تعريفه على أنه :
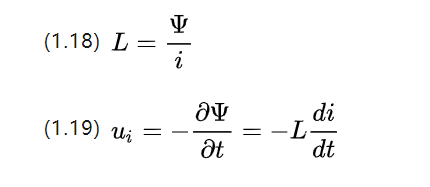
i هي شدة التيار المتغيرة ، L هي معامل الحث الذاتي في Henry [H] ، ويرتبط حجمها بشكل حجم الملف وعدد الدورات والنفاذية المغناطيسية.
تصنع الملفات في المحركات الحثية بحيث تحتوي على مادة مغناطيسية حديدية في منتصف الملف ، مثل قلب حديدي ، من أجل زيادة النفاذية المغناطيسية ، بحيث يتم لف الملف على قلب الحديد ، ومن هنا جاء اسم الملف.
بالنسبة لقسم من مادة متجانسة خطيًا ، يمكن تقريب معامل الحث الذاتي الخاص بها بالمعادلة التالية
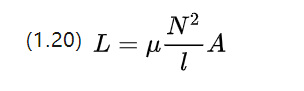
الحث الذاتي عبارة عن ملف من التغييرات الحالية الخاصة به للحث على ظاهرة كبت الجهد ، وميله إلى إعاقة التغيرات الحالية حول المحرك الكهربائي للتيار المستمر.
عندما يقترب ملفان من بعضهما البعض ، بالإضافة إلى الحث الذاتي الخاص بهم ، ولكن أيضًا بسبب الملفات المجاورة على التغييرات الحالية والحث المتبادل
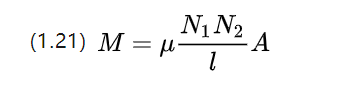
يتم تقريب معامل الحث المتبادل للمواد ذات الهويات الخطية بالمعادلة أعلاه ، والتي توضح أن الحث المتبادل يتأثر بعدد لفات الملفين في نفس الوقت.
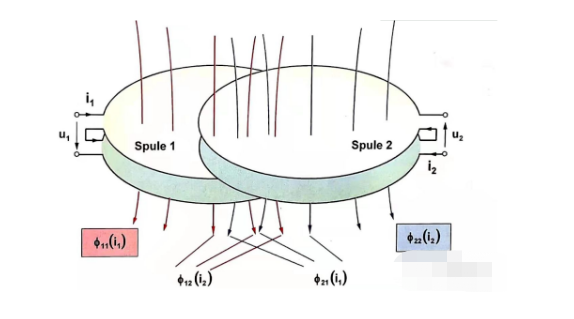
تجاهل المقاومة وفحص الحث الذاتي والمتبادل للملفين المتجاورين ، يمكن إدراج معادلة الجهد من الشكل 1.5 حول محركات التيار المستمر
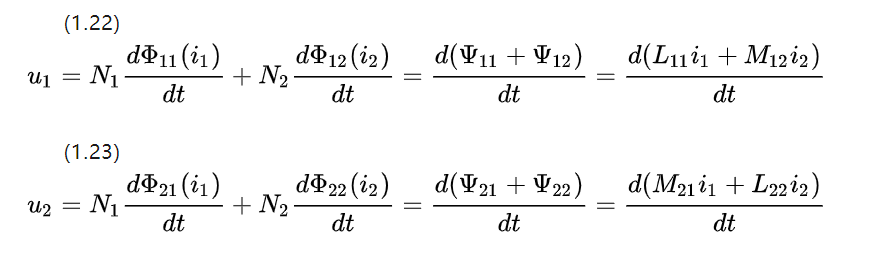
نظرًا لأن أجزاء التوصيل لها نفس معلمات المواد والشكل ، فإن معاملات الحث المتبادل الناتجة تكون متساوية M12 = M21.
لذا فإن حجم سلاسل التوصيل على كل ملف يتناسب مع القوة الحالية على ملف اللفات الدوار المقابل لمحرك التيار المستمر ..
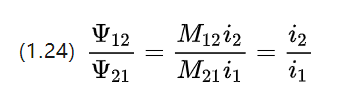
1.5 نظرية أوم للطاقة الكهربائية والدوائر المغناطيسية
درسنا في المدرسة الثانوية نظرية أوم، التي تنص على أن مقاومة الموصل هي نسبة الجهد والتيار عند كلا الطرفين، وأن هناك صيغة لوصف المادة المقاومة نفسها.
Q ، وهي الموصلية ، والتي هي بالضبط مقلوبة للمقاومة P وتصف القدرة على إجراء التيار.
بالإضافة إلى تطبيق المقاومة ، يمكن أيضًا وصف العلاقة بين الجهد والتيار باستخدام صورة التوصيل عندما يعمل المحرك الكهربائي.
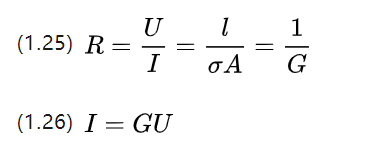
الآن قم بفحص شدة التيار لكل وحدة مساحة ، أي كثافة التيار J = I / A e (e هو متجه الوحدة) ، مع كثافة التيار كمتجه يشير إلى اتجاه التيار لمحركات التيار المتردد.
يمكن دمج هذا مع معادلة الجهد U = E.l و (1.25) المعاد كتابتها (1.26) كـ
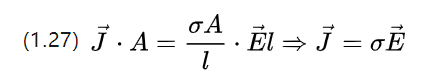
تصف المعادلة أعلاه نظرية أوم على المستوى المجهري، أي تغير كثافة التيار المقابلة لقوة مجال ثابتة مطبقة على الموصل.
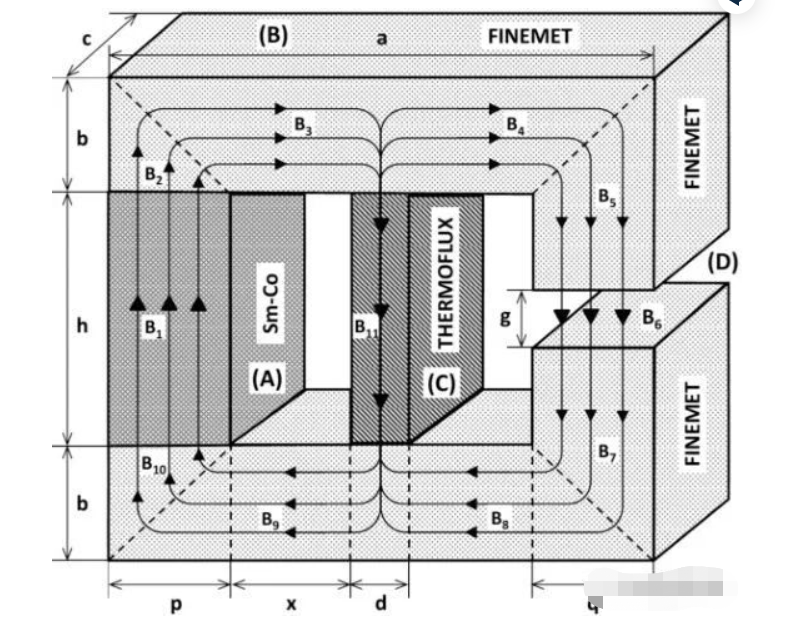
Lm هو الطول الفعال للتدفق المغناطيسي عبر قسم من الدائرة المغناطيسية ، و A هي منطقة التدفق المقابلة.
المعادلة أعلاه تشبه إلى حد بعيد صيغة المقاومة.
دعونا نشوه صيغة المقاومة المغناطيسية مرة أخرى ويمكننا الاستمرار في الحصول عليها
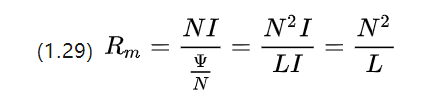
يمكن ملاحظة أن المقاومة المغناطيسية بالوحدات هي في الواقع معكوس معامل الحث.
استمرارًا للتماثل مع مفهوم الموصلية ، نحصل على الموصلية المغناطيسية A (magnetische Leitwert ، في [H] أو [Ωs])
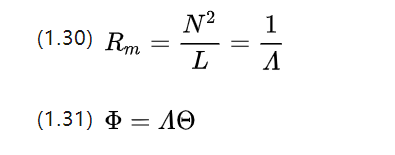
في الدائرة نجد العناصر التفاضلية لـ (1.26) ونحصل على نظرية أوم المجهرية، فما هي نظرية أوم المجهرية المقابلة للدائرة المغناطيسية؟
يمكننا المضي قدمًا في إعادة كتابة المعادلة (1.31) ، مع ملاحظة أن التدفق المغناطيسي نفسه له كثافة تدفق B ، والتي تنتج بعد ذلك
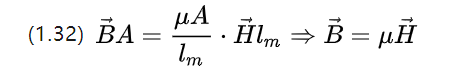
لذا فإن الدائرة المغناطيسية المجهرية نظرية أوم هي المعادلة (1.10)، وشدة المجال المغناطيسي تحتها هي كثافة التدفق الناتجة عن مغنطة مجال مغناطيسي ثابت.
يمكن استخدام التحليل الحسابي للمقاومة لتحقيق تحليل للعناصر الدقيقة للتدفق في عمود لف المحرك بأكمله ، والجزء الأساسي وجزء فجوة الهواء الوسيطة ، والتي يمكن أن تحقق تحليل عنصر محدود منفصل FEM (محدد - عنصر - ميثود) من الدائرة المغناطيسية بأكملها.
من الممكن أيضًا تطبيق نظرية كيرشوف للدائرة في الدائرة المغناطيسية، وهي بديهية ومريحة للغاية.
مرحبًا بكم في مشاركتنا المزيد من المعلومات حول المحركات الكهربائية في منطقة التعليقات!
في حالة وجود أي استفسار حول المحرك الكهربائي ، يرجى الاتصال بالمحرك الكهربائي المحترف الصانع في الصين على النحو التالي:

يحتوي محرك Dongchun على مجموعة واسعة من المحركات الكهربائية التي تُستخدم في صناعات مختلفة مثل النقل والبنية التحتية والبناء.
احصل على رد سريع.








